Séance 9-1-1 : Arithmétique dans Z - Partie 1 (Cours)

Sommaire

I- P.G.C.D - P.P.M.C

1-1/ Rappels et compléments

1-2/ Calcul pratique du P.G.C.D : algorithme d'euclide

1-3/ Nombres premiers entre eux

1-4/ Théorème de bezout

1-5/ Détermination des coefficients du théorème de bezout

1-6/ Applications du théorème de bezout

1-7/ L'équation diophantienne $ax+by=c$

1-8/ P.G.C.D et P.P.C.M d’un nombre fini d’entiers relatifs

1-9/ Congruence modulo n (rappels et compléments)

II- Les nombres premiers

2-1/ Rappels et compléments

2-2- Petit théorème de fermat

2-3/ Décomposition en produit de facteurs premiers

2-4/ Applications de la décomposition en produit de facteurs premiers

I- P.G.C.D - P.P.M.C

1-1/ Rappels et compléments

Définition 1

Soit $a$ et $b$ deux entiers relatifs non nulles.

Le plus grand commun diviseur de $a$ et $b$, noté $a\wedge b$ ou $PGCD(a,b)$, est le plus grand des
diviseurs positifs communs à $a$ et $b$.

Le plus petit commun multiple de $a$ et $b$, noté $a\vee b$ ou $PPCM(a,b)$, est le plus petit des multiples strictement positifs communs à $a$ et $b$.

On convient que : $a\wedge 0=\left|a\right|$ et $a\vee 0=0$

I- P.G.C.D - P.P.M.C

1-1/ Rappels et compléments

Remarques

Soit $a$ et $b$ deux entiers relatifs non nulles. Si $d=a\wedge b$ et $m=a\vee b$ alors :

- $d\ge 1$ et $d/a$ et $d/b$

- $m\ge 1$ et $a/m$ et $b/m$

- Pour toute $c\in \mathrm{\mathbb{N}}*$ : $\left[\left(c/a et c/b\right)\Rightarrow c/d\right]$ et $\left[\left(a/c et b/c\right)\Rightarrow m/c\right]$

- Pour toute $c\in \mathrm{\mathbb{N}}*$ : $\left[\left(c/a et c/b\right)\Rightarrow c\le d\right]$ et $\left[\left(a/c et b/c\right)\Rightarrow m\le c\right]$

- $\left|a\right|\wedge \left|b\right|=d$ et $a\wedge 1=1$ et $a\wedge a=a\wedge 0=\left|a\right|$

- $\left|a\right|\vee \left|b\right|=m$ et $a\vee 1=\left|a\right|$ et $a\vee a=\left|a\right|$

I- P.G.C.D - P.P.M.C

1-1/ Rappels et compléments

Proposition 1

Soit $a$, $b$ et $c$ des entiers relatifs non nulles et $n$ un entier naturel. Alors :

I- P.G.C.D - P.P.M.C

1-2/ Calcul pratique du P.G.C.D : algorithme d'euclide

Proposition 2

Soit $a\in \mathrm{\mathbb{Z}}*$ et $b\in \mathrm{\mathbb{N}}*$.

Lorsque $b$ ne divise pas $a$, le plus grand commun diviseur des entiers $a$ et $b$ est égal au dernier reste non nul obtenu grâce à l'algorithme d'Euclide.

I- P.G.C.D - P.P.M.C

1-3/ Nombres premiers entre eux

Définition 2

Soit $a$ et $b$ deux entiers relatifs non nulles.

On dit que $a$ et $b$ sont premiers entre eux si le seul diviseur positif commun à $a$ et $b$ est $1$, c'est-à-dire si $a\wedge b=1$:

I- P.G.C.D - P.P.M.C

1-3/ Nombres premiers entre eux

Théorème 1

Soit $a$ et $b$ deux entiers relatifs non nulles, et $d$ un entier naturel non nul.

Alors :

$d=a\wedge b\iff \left[\left(\exists \left(\alpha ;\beta \right)\in {\mathrm{\mathbb{Z}}}^2\right) a=\alpha d et b=\beta d et \alpha \wedge \beta =1\right]$

I- P.G.C.D - P.P.M.C

1-3/ Nombres premiers entre eux

Théorème 2

Soit $\left(a,b\right)\in {\left(\mathrm{\mathbb{Z}}*\right)}^2$

On a l’implication :

$d=a\wedge b\iff \left[\left(\exists \left(u;v\right)\in {\mathrm{\mathbb{Z}}}^2\right) d=au+bv\right]$

I- P.G.C.D - P.P.M.C

1-3/ Nombres premiers entre eux

Remarques

Le couple $\left(u;v\right)$ n'est pas unique. Par exemple :

$$\begin{gathered} 9\wedge 4=1=1\times 9-2\times 4 \left(u=1 et v=-2\right) \\ 9\wedge 4=\left(-43\right)\times 9+97\times 4 \left(u=-43 et v=97\right) \end{gathered}$$

La réciproque du théorème 2 est incorrecte, contre-exemple : $3\times 5+7\times \left(-1\right)=8$ mais $3\wedge 7\ne 8$.

I- P.G.C.D - P.P.M.C

1-4/ Théorème de bezout

Théorème 3

Soit $a$ et $b$ deux entiers relatifs non nulles.

Alors : $a\wedge b=1\iff \left[\left(\exists \left(u;v\right)\in {\mathrm{\mathbb{Z}}}^2\right) au+bv=1\right]$

I- P.G.C.D - P.P.M.C

1-4/ Théorème de bezout

Applications

En utilisant le théorème de Bezout, montrer que pour tout $n\in \mathrm{\mathbb{N}}$ :

$$\begin{gathered} \overline{)1} \left(5n+3\right)\wedge \left(2n+1\right)=1 \\ \overline{)2} \left(2n-1\right)\wedge \left(3-7n\right)=1 \end{gathered}$$

I- P.G.C.D - P.P.M.C

1-5/ Détermination des coefficients du théorème de bezout

L’inconvénient du théorème du Bezout, sous sa forme théorique, est qu’il ne fournit pas les coefficients $u$ et $v$ intervenant dans la relation $au+bv=1$.

L’algorithme d’Euclide fournit une réponse pratique à ce problème.

À titre d’exemple, posons : $a=155$ et $b=23$.

I- P.G.C.D - P.P.M.C

1-6/ Applications du théorème de bezout

Théorème 4

Soit $a$, $b$ et $c$ des entiers relatifs non nuls.

On a l’implication : $\left(a/bc et a\wedge b=1\right)\Rightarrow a/c$

Ce résultat est connu sous le nom de « Théorème de Gauss ».

Remarque

Dans le théorème de Gauss, la condition $a\wedge b=1$ est nécessaire.

Par exemple : $12/9\times 8$ mais $12$ ne divise ni le nombre $9$ ni le nombre $8$.

I- P.G.C.D - P.P.M.C

1-6/ Applications du théorème de bezout

Théorème 5

Soit $a$, $b$ et $c$ des entiers relatifs non nuls.

On a l’implication : $\left(a/c et b/c et a\wedge b=1\right)\Rightarrow ab/c$

Remarque

Dans le théorème 5, la condition $a\wedge b=1$ est nécessaire.

Par exemple : $8/48$ et $12/48$ mais $12\times 8$ ne divise pas $48$.

I- P.G.C.D - P.P.M.C

1-6/ Applications du théorème de bezout

Proposition 3

Soit $a$, $b$ et $c$ des entiers relatifs non nuls.

Alors :

1- $\left(a\wedge b=1 et a\wedge c=1\right)\iff a\wedge bc=1$

2- Pour tout $\left(m,n\right)\in {\left(\mathrm{\mathbb{N}}*\right)}^2$ : $\left(a\wedge b=1\iff a\wedge b^n=1\right)$ et $\left(a\wedge b=1\iff a^m\wedge b^n=1\right)$

I- P.G.C.D - P.P.M.C

1-7/ L'équation diophantienne $ax+by=c$

Théorème 6

Soit $a$, $b$ et $c$ des entiers relatifs tels que $ab\ne 0$

L’équation d’inconnue $ax+by=c$ a des solutions si, et seulement si, $a\wedge b$ divise $c$.

I- P.G.C.D - P.P.M.C

1-7/ L'équation diophantienne $ax+by=c$

Théorème 7

Si le couple $(x_0;y_0)$ est une solution de l’équation $\left(E\right) : ax+by=c$, alors l’ensemble solution de l’équation $\left(E\right)$ s’écrit sous la forme :

$S=\left\{\left(x_0+\frac{bk}{a\wedge b};y_0-\frac{ak}{a\wedge b}\right)/k\in \mathrm{\mathbb{Z}}\right\}$

I- P.G.C.D - P.P.M.C

1-8/ P.G.C.D et P.P.C.M d’un nombre fini d’entiers relatifs

Définition 3

Soit $n$ un entier naturel, $n\ge 2$, et des entiers relatifs non nuls $a_1,a_2,...a_n$

Le plus grand commun diviseur des entiers $a_1,a_2,...a_n$, noté $a_1\wedge a_2\wedge ...\wedge a_n$, est le plus grand des diviseurs positifs communs à $a_1,a_2,...a_n$.

Le plus petit commun multiple des entiers $a_1,a_2,...a_n$, noté $a_1\vee a_2\vee ...\vee a_n$ ou $PPCM\left(a_1,a_2,...a_n\right)$, est le plus petit des multiples positifs communs $a_1,a_2,...a_n$.

I- P.G.C.D - P.P.M.C

1-8/ P.G.C.D et P.P.C.M d’un nombre fini d’entiers relatifs

Théorème 8

Soit $n$ un entier naturel, $n\ge 2$, et des entiers relatifs non nuls $a_1,a_2,...a_n$.

I1 existe des entiers relatifs $u_1,u_2,...u_n$ tels que : $\sum _{i=1}^n{a}_i.u_i=\delta$, où $\delta$ désigne le plus grand commun diviseur de $a_1,a_2,...a_n$.

I- P.G.C.D - P.P.M.C

1-8/ P.G.C.D et P.P.C.M d’un nombre fini d’entiers relatifs

Définition 4

Soit $n$ un entier naturel, $n\ge 2$, et des entiers relatifs non nuls $a_1,a_2,...a_n$.

On dit que les entiers $a_1,a_2,...a_n$ sont premiers entre eux si $1$ est le seul diviseur positif commun à tous ces entiers, c'est-à-dire : $a_1\wedge a_2\wedge ...\wedge a_n=1$

I- P.G.C.D - P.P.M.C

1-8/ P.G.C.D et P.P.C.M d’un nombre fini d’entiers relatifs

Remarques

Attention, dire que des entiers sont premiers entre eux ne signifie pas qu’ils sont entre eux deux à deux. Par exemple, les trois entiers $a=8$, $b=7$ et $c=12$ sont premiers entre eux. Pourtant, les entiers $a$ et $c$ ont $4$ pour grand diviseur commun : $a\wedge c=4>1$

La relation $\left(a\vee b\right).\left(a\wedge b\right)=\left|ab\right|$ n’est pas valable pour plus de deux entiers relatifs.

Contre-exemple : $6\vee 10\vee 15=30$ et $6\wedge 10\wedge 15=1$

donc : $\left(6\vee 10\vee 15\right).\left(6\wedge 10\wedge 15\right)=30\ne 6\times 10\times 15$

c'est-à-dire qu’on a en général : $\left(a\vee b\vee c\right).\left(a\wedge b\wedge c\right)\ne \left|abc\right|$

Le résultat du théorème 8 reste aussi valable pour plus de deux entiers. Plus précisément : $\left(n\ge 2\right) \delta =a_1\wedge a_2\wedge ...\wedge a_n$ signifie qu’il existe $\left(a{\text{'}}_1,a{\text{'}}_2,...a{\text{'}}_n\right)\in {\mathrm{\mathbb{Z}}}^n$ tel que pour tout $i\in \left\{1;2;...;n\right\}$ : $a_i=\delta a{\text{'}}_i$ et $a{\text{'}}_1\wedge a{\text{'}}_2\wedge ...\wedge a{\text{'}}_n=1$.

I- P.G.C.D - P.P.M.C

1-8/ P.G.C.D et P.P.C.M d’un nombre fini d’entiers relatifs

Théorème 9

Soit $n$ un entier naturel, $n\ge 2$, et des entiers relatifs non nuls $a_1,a_2,...a_n$.

Les entiers $a_1,a_2,...a_n$ sont premiers entre eux si, et seulement si :

$\exists \left(u_1;u_2;...u_n\right)\in {\mathrm{\mathbb{Z}}}^n ; \sum _{i=1}^n{a}_i.u_i=1$

Autrement dit :

$\left(a_1\wedge a_2\wedge ...\wedge a_n=1\right)\iff \left[\exists \left(u_1;u_2;...u_n\right)\in {\mathrm{\mathbb{Z}}}^n ; \sum _{i=1}^n{a}_i.u_i=1\right]$

I- P.G.C.D - P.P.M.C

1-9/ Congruence modulo n (rappels et compléments)

Définition 5

Soit $n$ un entier naturel non nul.

On dit que deux entiers relatifs $a$ et $b$ sont congrus modulo $n$ si $n$ divise $b-a$, c'est-à-dire s'il existe un entier $k\in \mathrm{\mathbb{Z}}$ tel que $b=a+kn$.

On écrit : $a\equiv b \left[n\right]$

I- P.G.C.D - P.P.M.C

1-9/ Congruence modulo n (rappels et compléments)

Proposition 4

Soit $n$ un entier naturel non nul.

La relation « de congruence» est une relation d'équivalence sur $\mathrm{\mathbb{Z}}$, c'est-à-dire :

1) Elle est réflexive : $\left(\forall a\in \mathrm{\mathbb{Z}}\right) a\equiv a \left[n\right]$

2) Elle est symétrique : $\left(\forall \left(a;b\right)\in {\mathrm{\mathbb{Z}}}^2\right) \left(a\equiv b \left[n\right]\Rightarrow b\equiv a \left[n\right]\right)$

3) Elle est transitive : $\left(\forall \left(a;b;c\right)\in {\mathrm{\mathbb{Z}}}^3\right) \left(a\equiv b \left[n\right] et b\equiv c \left[n\right]\Rightarrow a\equiv c \left[n\right]\right)$

I- P.G.C.D - P.P.M.C

1-9/ Congruence modulo n (rappels et compléments)

Proposition 5

Soit $n$ un entier naturel non nul et $\left(a;b;c;d\right)\in {\mathrm{\mathbb{Z}}}^4$. Alors :

1) $a\equiv b \left[n\right]\iff$(Les restes respectifs des divisions euclidiennes de $a$ et $b$ par $n$ sont égaux)

2) Si $a\equiv b \left[n\right]$ et $c\equiv d \left[n\right]$, alors : $a+c\equiv b+d \left[n\right]$ et $ac\equiv bd \left[n\right]$.

3) Si $a\equiv b \left[n\right]$ et $k\in \mathrm{\mathbb{Z}}$, alors : $ka\equiv kb \left[n\right]$

4) Si $a\equiv b \left[n\right]$ et $p\in \mathrm{\mathbb{N}}$, alors : $a^p\equiv b^p \left[n\right]$

I- P.G.C.D - P.P.M.C

1-9/ Congruence modulo n (rappels et compléments)

Théorème 10

Soit $a$, $b$ et $c$ des entiers relatifs non nulles et $n\in \mathrm{\mathbb{N}}*$.

Si $d=c\wedge n$ alors :

$ac\equiv bc \left[n\right]\iff a\equiv b \left[\frac{n}{d}\right]$

I- P.G.C.D - P.P.M.C

1-9/ Congruence modulo n (rappels et compléments)

Proposition 6

Soit $a$, $b$ et $c$ des entiers relatifs non nuls et $\left(n;p\right)\in {\left(\mathrm{\mathbb{N}}*\right)}^2$ tels que $c\wedge n=1$

Alors :

$$\begin{gathered} \overline{)1} ac\equiv bc \left[n\right]\iff a\equiv b \left[n\right] \\ \overline{)2} \left\{\begin{array}{l}a\equiv b \left[n\right]\\ p/n\end{array}\right.\Rightarrow a\equiv b \left[p\right] \\ \overline{)3} \left\{\begin{array}{c}ac\equiv bc \left[p\right]\\ p premier\\ p ne divise pas c\end{array}\right.\Rightarrow a\equiv b \left[p\right] \end{gathered}$$

II- Les nombres premiers

2-1/ Rappels et compléments

Définition 6

Un entier relatif $p$ est dit premier lorsqu’il admet exactement quatre diviseurs.

Remarques

Si $p$ est un entier premier dans $\mathrm{\mathbb{N}}$, alors $-p$ est premier dans $\mathrm{\mathbb{Z}}$. C’est pourquoi dans cette section, nous nous limitons à l'ensemble $\mathrm{\mathbb{N}}$ des entiers naturels.

L’ensemble des nombres premiers (positifs) est noté $\mathrm{\mathbb{P}}$.

Un entier $n\ge 2$ non premier est dit composé.

II- Les nombres premiers

2-1/ Rappels et compléments

Théorème 11

Soit $n$ un entier composé supérieur ou égal à $2$. Alors :

1) Le plus petit diviseur positif de n différent de $1$ est un nombre premier.

2) $n$ est un produit de nombres premiers. En particulier, $n$ possède au moins un diviseur premier.

3) $n$ possède un facteur premier $p$ tel que $p^2\le n$.

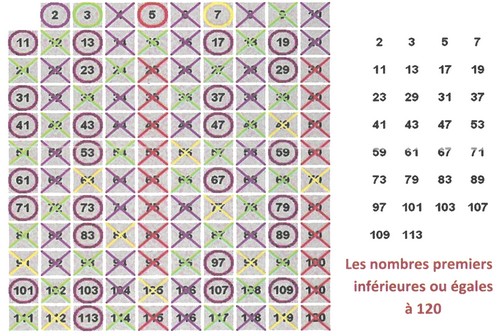
II- Les nombres premiers

2-1/ Rappels et compléments

Théorème 12

L'ensemble $\mathrm{\mathbb{P}}$ des nombres premiers positifs est infini.

II- Les nombres premiers

2-1/ Rappels et compléments

Théorème 13

1) Si $p$ et $q$ sont deux nombres premiers positifs distincts, alors ils sont premiers entre eux.

En d’autres termes : $\left(p\in \mathrm{\mathbb{P}} et q\in \mathrm{\mathbb{P}} et p\ne q\right)\Rightarrow p\wedge q=1$

2) Si $p\in \mathrm{\mathbb{P}}$, alors $p$ est premier avec tous les entiers qu'il ne divise pas.

En d'autres termes : $\left(\forall a\in \mathrm{\mathbb{Z}}\right) \left(\forall p\in \mathrm{\mathbb{P}}\right) \left[\left(p ne divise pas a\right)\Rightarrow p\wedge a=1\right]$

II- Les nombres premiers

2-1/ Rappels et compléments

Proposition 7

Soit $\left(a,b\right)\in {\mathrm{\mathbb{Z}}}^2$ et $p$ un nombre premier. Alors :

$p/ab\iff \left(p/a ou p/b\right)$

II- Les nombres premiers

2-1/ Rappels et compléments

Corollaire

Soit $a_1,a_2,...a_n$ des entiers relatifs et $p$ un nombre premier. Alors :

$p/a_1.a_2....a_n\iff \left(\exists i\in \left\{1;2;...;n\right\} p/a_i\right)$

Soit $a\in \mathrm{\mathbb{Z}}$ et $p$ un nombre premier. Alors :

$\left(\forall n\in \mathrm{\mathbb{N}}*\right) p/a^n\iff p/a$

Soit $p_1,p_2,...,p_n$ et $p$ des nombres premiers. Alors :

$p/p_1.p_2....p_n\iff \left(\exists i\in \left\{1;2;...;n\right\} p=p_i\right)$

II- Les nombres premiers

2-2- Petit théorème de fermat

Théorème 14

1) Si $p$ est un nombre premier positif, alors il divise $a^p-a$, pour tout $a\in \mathrm{\mathbb{Z}}$.

Autrement dit : $\left(\forall a\in \mathrm{\mathbb{Z}}\right) a^p\equiv a \left[p\right]$

2) Si $p$ est un nombre premier positif, alors pour tout $a\in \mathrm{\mathbb{Z}}$ : $p\wedge a=1\Rightarrow a^{p-1}\equiv 1 \left[p\right]$

II- Les nombres premiers

2-2- Petit théorème de fermat

Remarques

La réciproque du petit théorème de Fermat n'est pas vraie. Autrement dit, si $a^{p-1}\equiv 1 \left[p\right]$, alors l’entier $p$ n'est pas nécessairement premier. A titre d’exemple, le nombre $p=341=31\times 11$ n’est pas premier, or, il divise $2^{341}-2$ car :

$2^{341}-2=2\left(2^{340}-1\right)=2\left({\left(2^{10}\right)}^{34}-1\right)=2\left(2^{10}-1\right)\sum _{k=0}^{33}{2}^{10k}=2\times 3\times 341\times \sum _{k=0}^{33}{2}^{10k}$

Le petit théorème de Fermat permet de calculer le reste de n'importe quel entier assez grand modulo un nombre premier positif $p$.

II- Les nombres premiers

2-3/ Décomposition en produit de facteurs premiers

Théorème 15

Tout élément de $\mathrm{\mathbb{Z}}*-\left\{1;-1\right\}$ admet une décomposition en produit de nombres premiers, unique à
l’ordre près des facteurs.

Autrement dit, si $n\in \mathrm{\mathbb{Z}}*-\left\{1;-1\right\}$, il existe $N\in \mathrm{\mathbb{N}}*$, $\epsilon \in \left\{1;-1\right\}$, des nombres premiers deux à deux distincts $p_1,p_2,...p_N$, et des entiers ${\alpha }_1,{\alpha }_2,...{\alpha }_N$ tels que : $n=\epsilon .{p_1}^{{\alpha }_1}.{p_2}^{{\alpha }_2}...{p_N}^{{\alpha }_N}$

Ce théorème est connu sous le nom « Théorème fondamental de l'arithmétique ».

II- Les nombres premiers

2-4/ Applications de la décomposition en produit de facteurs premiers

Théorème 16

Soit $n\in \mathrm{\mathbb{Z}}*-\left\{1;-1\right\}$ et sa décomposition $n=\epsilon .{p_1}^{{\alpha }_1}.{p_2}^{{\alpha }_2}...{p_N}^{{\alpha }_N}$ en produit de facteurs premiers.

Les diviseurs de $n$ sont les entiers relatifs : $d=\epsilon \text{'}.{p_1}^{{\gamma }_1}.{p_2}^{{\gamma }_2}...{p_N}^{{\gamma }_N}$ avec $\forall k\in \left\{1;2;...;N\right\} 0\le {\gamma }_k\le {\alpha }_k$ et $\epsilon \text{'}\in \left\{1;-1\right\}$

Le nombre de diviseurs positifs de $n$ est : $\left(1+{\alpha }_1\right)\left(1+{\alpha }_2\right)...\left(1+{\alpha }_n\right)$