Séance 7-2-1 : Calcul intégral - Partie 2 (Cours)

Sommaire

IV- Intégration et ordre

4-1/ Positivité et croissance

4-2/ Intégrale et valeur absolue

4-3/ Valeur moyenne d'une fonction continue sur un segment

V- Applications du calcul intégral

5-1/ Calcul des aires

5-2/ Calcul des volumes

5-3/ Encadrement d’une intégrale par deux suites (méthode des rectangles)

IV- Intégration et ordre

4-1/ Positivité et croissance

Proposition 6

Soit $f$ et $g$ deux fonctions continues sur un segment $\left[a;b\right] \left(a<b\right)$.

Si $f$ est positive sur $\left[a;b\right]$ alors : ${\int }_a^{b}f\left(x\right)dx\ge 0$

Si $f\left(x\right)\le g\left(x\right)$ pour tout $x\in \left[a;b\right]$, alors : ${\int }_a^{b}f\left(x\right)dx\le {\int }_a^{b}g\left(x\right)dx$

IV- Intégration et ordre

4-1/ Positivité et croissance

Applications

1. Montrer que $0\le {\int }_1^{\frac{\mathrm{\pi }}{2}}\frac{\sin t}{t}dt\le \frac{\mathrm{\pi }}{2}-1$ et $\frac{\mathrm{\pi }}{3}\le {\int }_0^{\frac{\mathrm{\pi }}{3}}\frac{1+t}{\cos t}dt\le \frac{2{\mathrm{\pi }}^2}{9}+\frac{2\mathrm{\pi }}{3}$.

2. Montrer que pour tout $x\in {\mathrm{ℝ}}_{+}^{*}$ : $0\le {\int }_x^{2x}\frac{dt}{\sqrt{t^4+t^2+1}}\le \frac{1}{x}$

Pour tout $n\in \mathrm{\mathbb{N}}$, on pose $I_n={\int }_0^{\frac{\mathrm{\pi }}{6}}{x}^n\cos \left(3x\right)dx$

3. Montrer que la suite $\left(I_n\right)$ est décroissante.

4. Montrer que pour tout $n\in \mathrm{\mathbb{N}}$ : $0\le I_n\le {\left(\frac{\mathrm{\pi }}{6}\right)}^{n+1}$

5. En déduire $\underset{n\to \infty }{\lim }{I}_n$

IV- Intégration et ordre

4-2/ Intégrale et valeur absolue

Proposition 7

Soit $f$ une fonction continue sur un intervalle $I$, et soit $\left(a;b\right)\in I^2$ tel que $a\le b$.

On a alors : $\left|{\int }_a^{b}f\left(x\right)dx\right|\le {\int }_a^b\left|f\left(x\right)\right|dx$

IV- Intégration et ordre

4-3/ Valeur moyenne d'une fonction continue sur un segment

Proposition 8

Soit $f$ une fonction continue sur un intervalle $I$, et soit $\left(a;b\right)\in I^2$ tel que $a\le b$.

S’il existe deux réels $m$ et $M$ tels que pour tout $x\in \left[a;b\right]$ : $m\le f\left(x\right)\le M$, alors :

$m\left(b-a\right)\le {\int }_a^{b}f\left(x\right)dx\le M\left(b-a\right)$

S’il existe un réel $M$ tels que pour tout $x\in \left[a;b\right]$ : $\left|f\left(x\right)\right|\le M$, alors :

$\left|{\int }_a^{b}f\left(x\right)dx\right|\le M\left(b-a\right)$

IV- Intégration et ordre

4-3/ Valeur moyenne d'une fonction continue sur un segment

Définition 1

Soit $f$ une fonction continue sur un segment $\left[a;b\right] \left(a<b\right)$

La valeur moyenne de la fonction $f$ sur $\left[a;b\right]$ est le nombre réel $\mu =\frac{1}{b-a}{\int }_a^{b}f\left(x\right)dx$.

IV- Intégration et ordre

4-3/ Valeur moyenne d'une fonction continue sur un segment

Proposition 9

Soit $f$ une fonction continue sur un segment $\left[a;b\right] \left(a<b\right)$.

Il existe au moins un réel $c\in \left[a;b\right]$ tel que : ${\int }_a^{b}f\left(x\right)dx=\left(b-a\right)f\left(c\right)$

Ce résultat porte le nom de « Théorème de la moyenne »

IV- Intégration et ordre

4-3/ Valeur moyenne d'une fonction continue sur un segment

Remarques

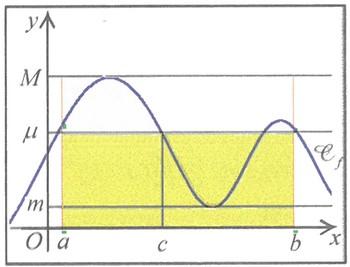
Si $f\left(\left[a;b\right] \right)=\left[m;M\right]$ et $F$ désigne une primitive de la fonction $f$ sur $\left[a;b\right]$, alors la formule ${\int }_a^{b}f\left(x\right)dx=\left(b-a\right)f\left(c\right)$ est équivalente à $F\left(b\right)-F\left(A\right)=\left(b-a\right)F\text{'}\left(c\right)$, et cette formule n’est qu’une copie de la formule du théorème des accroissements finis appliquée à la fonction $F$.

Graphiquement, une interprétation de ce théorème est que l'aire algébrique sous la courbe ${\mathcal{C}}_f$ est égale à celle d'un rectangle de base $\left[a;b\right]$, et de hauteur l’ordonnée d’un point moyen de la courbe.

V- Applications du calcul intégral

5-1/ Calcul des aires

Proposition 10

Soit $f$ une fonction continue sur un segment $\left[a;b\right] \left(a<b\right)$, et ${\mathcal{C}}_f$ sa courbe représentative dans un
repère orthogonal.

L'aire du domaine délimité par , l'axe des abscisses et les droites d'équations $x=a$ et $x=b$ est égale à ${\int }_a^b\left|f\left(x\right)\right|dx$ (en unité d'aire).

V- Applications du calcul intégral

5-1/ Calcul des aires

Proposition 11

Le plan est rapporté à un repère orthogonal.

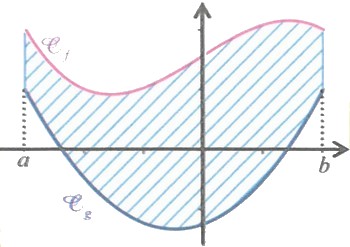
Soit $f$ et $g$ deux fonctions continues sur un segment $\left[a;b\right]$.

Soit ${\mathcal{C}}_f$ et ${\mathcal{C}}_g$ les courbes représentatives de $f$ et $g$.

Soit $\left(\Delta \right)$ le domaine délimité par les courbes ${\mathcal{C}}_f$ et ${\mathcal{C}}_g$ et les droites d'équations $x=a$ et $x=b$.

Alors : L'aire du domaine $\left(\Delta \right)$ en unités d'aire est donnée par : $\sigma \left(\Delta \right)={\int }_a^b\left|f\left(x\right)-g\left(x\right)\right|dx$

V- Applications du calcul intégral

5-2/ Calcul des volumes

Proposition 12

L'espace est rapporté à un repère orthonormé $\left(O;\overrightarrow{i};\overrightarrow{j};\overrightarrow{k}\right)$.

Soit $\left(a;b\right)\in {\mathrm{ℝ}}^2$ tel que $a<b$.

On considère un solide $\left(S\right)$ limité par deux plans parallèles au plan $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$ :

• le plan de cote $a$ d'équation $z=a$
• le plan de cote $b$ d'équation $z=b$

Si $S\left(t\right)$ est l'aire de l'intersection du solide $\left(S\right)$ avec tout plan parallèle $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$ de cote $t$, alors le volume de ce solide est (en unités de volume) : $v\left(S\right)={\int }_a^{b}S\left(t\right)dt$

V- Applications du calcul intégral

5-2/ Calcul des volumes

Proposition 13

L’espace est rapporté à un repère orthonormé $\left(O;\overrightarrow{i};\overrightarrow{j};\overrightarrow{k}\right)$.

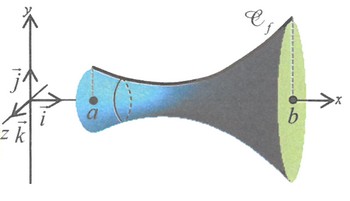
Soit $f$ une fonction continue sur un segment $\left[a,b\right] \left(a<b\right)$, et ${\mathcal{C}}_f$ sa courbe représentative dans le repère $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$.

Le volume du solide engendré par la rotation de la courbe ${\mathcal{C}}_f$ autour de l'axe des abscisses un tour complet est donné par la formule : $V=\mathrm{\pi }{\int }_a^b{\left(f\left(x\right)\right)}^{2}dx$ (en unités de volume)

V- Applications du calcul intégral

5-2/ Calcul des volumes

Proposition 14

Soit $f$ une fonction continue et strictement monotone sur un segment $\left[a,b\right] \left(a<b\right)$, et ${\mathcal{C}}_f$ sa courbe représentative dans un repère orthonormé $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$.

Le volume du solide engendré par la rotation de la courbe ${\mathcal{C}}_f$ autour de l'axe des ordonnées un tour complet est donné la formule : $V=\mathrm{\pi }\left|{\int }_{\mathrm{f}\left(a\right)}^{\mathrm{f}\left(b\right)}{\left(f^{-1}\left(x\right)\right)}^{2}dx\right|$ (en unité de volume)

Si de plus, $f$ est dérivable sur $\left[a,b\right]$ alors : $V=\mathrm{\pi }\left|{\int }_{\mathrm{a}}^{\mathrm{b}}{\mathrm{x}}^2\left|\mathrm{f}\text{'}\left(\mathrm{x}\right)\right|dx\right|$ (en unité de volume)

V- Applications du calcul intégral

5-3/ Encadrement d’une intégrale par deux suites (méthode des rectangles)

Proposition 15

Soit $f$ une fonction continue sur un segment $\left[a,b\right] \left(a<b\right)$.

Pour tout entier $n\ge 2$ on pose :

$x_0=a ; x_1=a+\frac{b-a}{n} ; ... ; x_k=a+k\frac{b-a}{n} ; ... ; x_n=a+n\frac{b-a}{n}=b$

Pour tout $k\in \left\{0,1,...,n-1\right\}$, on note $M_k$ la valeur maximale et $m_k$ la valeur minimale de $f$ sur le segment $\left[x_k;x_{k+1}\right]$.

On pose enfin ${\lambda }_n=\frac{b-a}{n}\sum _{k=0}^{n-1}{M}_k$  et ${\mu }_n=\frac{b-a}{n}\sum _{k=0}^{n-1}{m}_k$

On a alors pour tout entier $n\ge 2$ :

${\mathrm{\lambda }}_{\mathrm{n}}\le {\int }_a^b\mathrm{f}\left(\mathrm{x}\right)dx\le {\mu }_n$

V- Applications du calcul intégral

5-3/ Encadrement d’une intégrale par deux suites (méthode des rectangles)

Proposition 16

Soit $f$ une fonction continue sur un segment $\left[a,b\right] \left(a<b\right)$.

Pour tout entier $n\in \mathrm{\mathbb{N}}*$ on pose :

$s_n=\frac{b-a}{n}\sum _{k=0}^{n-1}f\left(a+k\frac{b-a}{n}\right)$ et $S_n=\frac{b-a}{n}\sum _{k=1}^{n}f\left(a+k\frac{b-a}{n}\right)$

Alors les deux suites ${\left(s_n\right)}_{n\ge 1}$ et ${\left(S_n\right)}_{n\ge 1}$ convergent et admettent ${\int }_a^b\mathrm{f}\left(\mathrm{x}\right)dx$ comme limite commune.

Autrement dit :

$\underset{n\to +\infty }{\lim }\frac{b-a}{n}\sum _{k=0}^{n-1}f\left(a+k\frac{b-a}{n}\right)=\underset{n\to +\infty }{\lim }\frac{b-a}{n}\sum _{k=1}^{n}f\left(a+k\frac{b-a}{n}\right)={\int }_a^b\mathrm{f}\left(\mathrm{x}\right)dx$

V- Applications du calcul intégral

5-3/ Encadrement d’une intégrale par deux suites (méthode des rectangles)

Applications

Calculer la limite :

$\underset{n\to +\infty }{\lim }n\sum _{k=0}^{n-1}\frac{1}{n^2+k^2}$