
Mathématiques : 2Bac SPC-SVT-Agro-STE-STM
Semestre 2 Devoir 2 Modèle 2
Professeur : Mr CHEDDADI Haitam
I- Exercice 1
Partie 1
Soit g la fonction numérique définie sur ℝ par : g(x)=ex-x2+3x-1
Le tableau suivant est le tableau de variations de la fonction g :
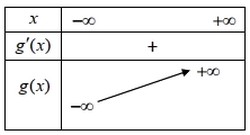
- Vérifier que g(0)=0.
- Déterminer le signe de g(x) sur chacun des intervalles ]-∞;0] et [0;+∞[.
Partie 2
Soit f la fonction numérique définie sur ℝ par : f(x)=(x2-x)e-x+x
Soit (Cf) sa courbe représentative dans un repère orthonormé (O,→i,→j) (unité : 1 cm).
- Vérifier que f(x)=x2ex-xex+x pour tout x de ℝ, puis montrer que limx→+∞f(x)=+∞.
- Calculer limx→+∞(f(x)-x), puis en déduire que (Cf) admet une asymptote (D) au voisinage de +∞ d’équation y=x.
- Vérifier que f(x)=x2-x+xexex pour tout x de ℝ, puis calculer limx→-∞f(x).
- Montrer que limx→-∞f(x)x=-∞, et interpréter le résultat géométriquement.
- Montrer que f(x)-x et x2-x ont le même signe pour tout x de ℝ.
- En déduire que (Cf) est au dessus de (D) sur chacun des intervalles ]-∞;0] et [1;+∞[, et en dessous de (D) sur l’intervalle [0;1].
- Montrer que f'(x)=g(x)e-x pour tout x de ℝ.
- En déduire que la fonction f est décroissante sur ]-∞;0] et croissante sur [0;+∞[.
- Dresser le tableau de variations de la fonction f.
- Vérifier que f"(x)=(x2-5x+4)e-x pour tout x de ℝ.
- En déduire que la courbe (Cf) admet deux points d’inflexion d’abscisses respectives 1 et 4.
- Construire (D) et (Cf) dans le même repère (O,→i,→j) (on prend : f(4)≈4.2)
- Montrer que la fonction H: x↦(x2+2x+2)e-x est une primitive de la fonction h: x↦-x2e-x sur ℝ, puis en déduire que ∫10x2e-xdx=2e-5e.
- À l’aide d’une intégration par parties, montrer que ∫10xe-xdx=e-2e.
- Calculer en cm2 l’aire du domaine plan limité par (Cf) et (D) et les droites d’équations x=0 et x=1.
Partie 3
Soit (un) la suite numérique définie par : {u0=12un+1=f(un)(∀n∈ℕ)
- Montrer que 0≤un≤1 pour tout n de ℕ (on pourra utiliser le résultat de la question 8).
- Montrer que la suite (un) est décroissante.
- En déduire que (un) est convergente et déterminer sa limite.
II- Exercice 2
On considère l’équation différentielle suivante : (E):y"-2y'+y=0
- Résoudre l’équation (E).
- Déterminer la fonction h qui vérifie l’équation (E) et sa courbe passe par le point O(0;0) et h'(0)=-1.
- Vérifie que la fonction g(x)=2-xex vérifie l’équation (E1):y"-2y'+y=2.


