Séance 17 - Quadrilatères particuliers

Sommaire

I- Le rectangle

1-1/ Définition

1-2/ Propriétés des diagonales

1-3/ Axes et centre de symétrie

II- Le losange

2-1/ Définition

2-2/ Propriétés des diagonales

2-3/ Axes et centre de symétrie

III- Le carré

3-1/ Définition

3-2/ Propriétés des diagonales

3-3/ Axes et centre de symétrie

IV- Synthèse

V- Exercices

5-1/ Exercice 1

5-2/ Exercice 2

5-3/ Exercice 3

5-4/ Exercice 4

5-5/ Exercice 5

5-6/ Exercice 6

5-7/ Exercice 7

I- Le rectangle

1-1/ Définition

Le rectangle est un parallélogramme qui a un angle droit.

Exemple

Soit $ABCD$ un rectangle.

Remarque importante

Toutes les propriétés du parallélogramme s’appliquent au rectangle.

I- Le rectangle

1-2/ Propriétés des diagonales

Propriété directe

Si un quadrilatère est un rectangle, alors ses diagonales ont même longueur.

Autrement dit :

Si $ABCD$ est un rectangle, alors : $AC=BD$.

I- Le rectangle

1-2/ Propriétés des diagonales

Propriété réciproque

Si les diagonales d'un parallélogramme ont même longueur, alors c'est un rectangle.

Autrement dit :

Si $ABCD$ est un parallélogramme tel que $AC=BD$, alors c'est un rectangle.

I- Le rectangle

1-3/ Axes et centre de symétrie

Les axes de symétrie d’un rectangle sont les médiatrices de ses côtés.

Le centre de symétrie d’un rectangle est son centre.

II- Le losange

2-1/ Définition

Le losange est un parallélogramme qui a deux côtés consécutifs de même longueur.

Exemple

Soit $ABCD$ un losange.

On a : $AB=BC ; BC=CD ; CD=DA ; DA=AB$

Remarque importante

Toutes les propriétés du parallélogramme s’appliquent au losange.

II- Le losange

2-2/ Propriétés des diagonales

Propriété directe

Si un quadrilatère est un losange, alors ses diagonales sont perpendiculaires.

Autrement dit :

Si $ABCD$ est un losange, alors : $\left(AC\right)\perp \left(BD\right)$.

II- Le losange

2-2/ Propriétés des diagonales

Propriété réciproque

Si les diagonales d'un parallélogramme sont perpendiculaires, alors c'est un losange.

Autrement dit :

Si $ABCD$ est un parallélogramme tel que $\left(AC\right)\perp \left(BD\right)$, alors c'est un losange.

II- Le losange

2-3/ Axes et centre de symétrie

Les axes de symétrie d’un losange sont ses diagonales.

Le centre de symétrie d’un losange est son centre.

III- Le carré

3-1/ Définition

Le carré est un parallélogramme qui a un angle droit et deux côtés consécutifs de même longueur.

Exemple

Soit $ABCD$ un carré.

Remarques importantes

Toutes les propriétés du parallélogramme s’appliquent au carré.

Le carré est à la fois un rectangle et un losange.

III- Le carré

3-2/ Propriétés des diagonales

Propriété directe

Si un quadrilatère est un carré, alors ses diagonales sont perpendiculaires et ont la même longueur.

Autrement dit :

Si $ABCD$ est un carré , alors : $AC=BD$ et $\left(AC\right)\perp \left(BD\right)$.

III- Le carré

3-2/ Propriétés des diagonales

Propriété réciproque

Si les diagonales d'un parallélogramme sont perpendiculaires et ont même longueur, alors c'est un carré.

Autrement dit :

Si $ABCD$ est un parallélogramme tel que $AC=BD$ et $\left(AC\right)\perp \left(BD\right)$, alors c'est un carré.

III- Le carré

3-3/ Axes et centre de symétrie

Les axes de symétrie d’une carré sont ses diagonales et les médiatrices de ses cotés.

Le centre de symétrie d’un carré est son centre.

IV- Synthèse

V- Exercices

5-1/ Exercice 1

$IJKL$ est un rectangle de centre $O$ tel que $\widehat{JLK}=40°$ et $OJ=2,2cm$.

1. Citer tous les triangles isocèles de la figure.

2. Citer tous les triangles rectangles de la figure.

3. Calculer les mesures suivantes :

$OL ; IK ; \widehat{OKL} ; \widehat{OLI} ; \widehat{LIO} ; \widehat{IJL}$

V- Exercices

5-2/ Exercice 2

1. Construire le point $D$ le symétrique de $A$ par rapport à $I$ sur la figure.

2. Prouver que $ABDC$ est un parallélogramme, puis déduire sa nature

3. Construire les points $F$ et $G$ les symétriques respectifs de $B$ et $C$ par rapport à $A$.

4. Prouver que le quadrilatère $FCBG$ est un losange.

V- Exercices

5-3/ Exercice 3

$ABC$ est un triangle isocèle en $A$.

$M$ est le milieu de $\left[BC\right]$.

Le point $D$ est le symétrique du point $A$ par rapport au point $M$.

1. Construire la figure.

2. Montrer que $ABDC$ est un losange.

V- Exercices

5-4/ Exercice 4

$ABCD$ est un carré de centre $O$.

1. Construire la figure.

2. Montrer que le triangle $AOB$ est un triangle rectangle.

3. Montrer que $AC=BD$.

V- Exercices

5-5/ Exercice 5

$ABCD$ est un carré de centre $O$.

Soient $M$ et $N$ les milieux respectifs des segments $\left[AB\right]$ et $\left[BC\right]$.

1. Construire $E$ le symétrique de $O$ par rapport à $M$.

2. Construire $F$ le symétrique de $O$ par rapport â $N$.

3. Montrer que $AEBO$ est un carré.

4. Démontrer que $OEF$ est un triangle isocèle.

V- Exercices

5-6/ Exercice 6

$ABCD$ et $ABEF$ sont deux parallélogrammes :

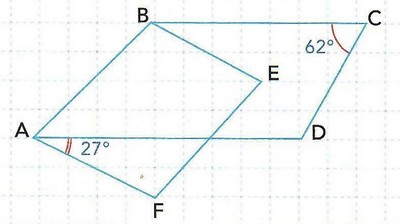
En utilisant les données de la figure, Hicham prétend que « $ABEF$ est rectangle ».

1. Qu'en pensez-vous ? Justifier.

V- Exercices

5-7/ Exercice 7

Dans la figure ci-dessous, $KEPI$ et $LORD$ sont deux parallélogrammes :

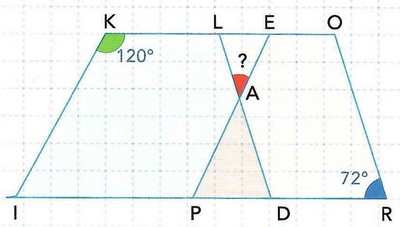
Les côtés $\left[LD\right]$ et $\left[EP\right]$ se coupent en $A$.

1. En utilisant les données de la figure, déterminer la mesure de $\widehat{LAE}$ (justifier).