Mathématiques : 2Bac Eco-SGC
Séance 8 (Primitive d’une fonction numérique)
Professeur : Mr ETTOUHAMY Abdelhak
Sommaire
I- Primitive d’une fonction sur un intervalle
1-1 Définition
1-2/ Proposition 1
1-3/ Proposition 2
2-3/ Proposition 3
II- primitives usuelles et opérations
III- Exercices
3-1/ Exercice 1
3-2/ Exercice 2
3-3/ Exercice 3
3-4/ Exercice 4
I- Primitive d’une fonction numérique sur un intervalle
1-1 Définition
Soit f et F deux fonctions définies sur un intervalle I de ℝ.
On dit que F est une primitive de la fonction f sur I si F est dérivable sur I et ∀x∈I : F'(x)=f(x)
Exemple
I- Primitive d’une fonction numérique sur un intervalle
1-2/ Proposition 1
Si f est une fonction continue sur un intervalle I de ℝ , alors f admet des primitives sur I.
Exemple
I- Primitive d’une fonction numérique sur un intervalle
1-3/ Proposition 2
Soit f une fonction continue sur un intervalle I de ℝ.
- Si F est une primitive de la fonction f sur I alors les primitives de sur I sont les fonctions x→F(x)+c ; (c∈ℝ)
- soient x0∈I et y0∈ℝ ; il existe une seule fonction primitive G de f qui vérifie la condition G(x0)=y0.
Exemple
I- Primitive d’une fonction numérique sur un intervalle
1-4/ Proposition 3
F et G sont les primitives respectivement de f et g sur I.
On a F+G est une primitive de f+g sur I.
Pour tout α,β∈ℝ, on a αF+βG est une primitive de αf+βg.
Exemple
II- primitives usuelles et opérations
2-1/ Tableau des primitives usuelles
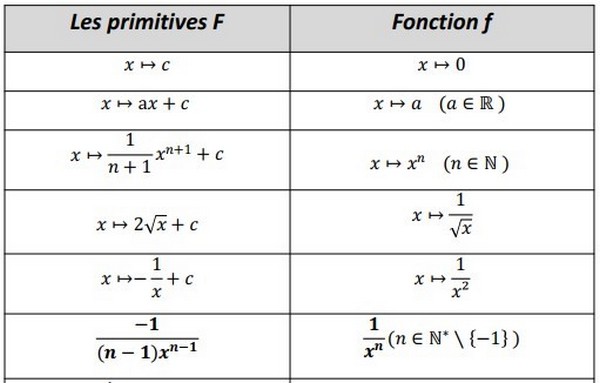
Exemple
II- primitives usuelles et opérations
2-2/ Fonctions primitives et opérations
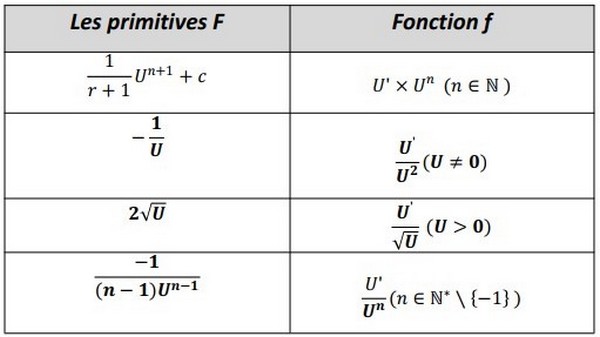
Exemple
III- Exercices
3-1/ Exercice 1
Soit f et F deux fonctions numériques.
Montrer que F est une primitive de f sur I dans les cas suivants :
1 (F(x)=x3+1x+4f(x)=3x2-1x2I=ℝ*)2 (F(x)=13x3+√x+4f(x)=x2+12√xI=]0,+∞[)3 (F(x)=(x2+1)33f(x)=2x(x2+1)2I=]0,+∞[)
III- Exercices
3-2/ Exercice 2
Soient f et F deux fonctions numériques définies sur ℝ par :
F(x)=x4+x3+x2+1f(x)=4x3+3x2+2xI=ℝ
- Montrer que F est une primitive de f sur ℝ.
- Déterminer G l’ensemble des primitives de f sur ℝ.
- Déterminer la primitive de f qui vérifie G(0)=1.
III- Exercices
3-3/ Exercice 3
Déterminer les primitives des fonctions suivantes :
| f1(x)=4x4+3x3+x ; I=ℝf2(x)=12√x+3 ; I=]0,+∞[f3(x)=2x5-3x2-1 ; I=ℝf4(x)=1x3+23x5 ; I=ℝ*f5(x)=2x(x2+1)3 ; I=ℝ | f6(x)=2x(x2+1)2 ; I=ℝf7(x)=2x√x2+1 ; I=ℝf8(x)=x(x2+1) ; I=ℝf9(x)=1x2(1x-1)3 ; I=ℝ* |
III- Exercices
3-4/ Exercice 4
Soit f la fonction définie sur ]-1;1[ par : f(x)=x2+1(x2-1)2
- Déterminer deux réels a et b tels que f(x)=ax(x2-1)2-b(x-1)2.
- En déduire toutes les primitives de f sur ]-1;1[.
- Déterminer la primitive F de la fonction f qui vérifie F(0)=1.
