
Mathématiques : 2Bac Eco-SGC
Séance 4 (Dérivabilité d’une fonction numérique)
Professeur : Mr ETTOUHAMY Abdelhak
Sommaire
I- Dérivabilité d’une fonction en un point
1-1/ Nombre dérivé en un point
1-2/ Interprétation géométrique du nombre dérivé
II- Dérivabilité à droite – dérivabilité à gauche
2-1/ Définition et propriété
2-2/ Interprétation géométrique
III- Dérivabilité d’une fonction sur un intervalle
3-1/ Définition
3-2/ Propriété
3-3/ Tableau des dérivées usuelles
3-4/ Opérations sur les fonctions dérivées
IV- Applications de la dérivation
4-1/ Variations d’une fonction
4-2/ Valeur minimale et maximale
4-3/ Étude de la concavité d’une courbe
V- Exercices
5-1/ Exercice 1
5-2/ Exercice 2
5-3/ Exercice 3
5-4/ Exercice 4
5-5/ Exercice 5
5-6/ Exercice 6
I- Dérivabilité d’une fonction en un point
1-1/ Nombre dérivé en un point
Définition
Soit une fonction définie sur un intervalle ouvert , et soit
On dit que est dérivable en , s’il existe un réel tel que :
Le nombre est appelé le nombre dérivé de la fonction en , noté , et on écrit :
Exemple
I- Dérivabilité d’une fonction en un point
1-2/ Interprétation géométrique du nombre dérivé
Propriété
Si est une fonction dérivable en , alors l’équation de la tangente à la courbe au point d’abscisse est donnée par :
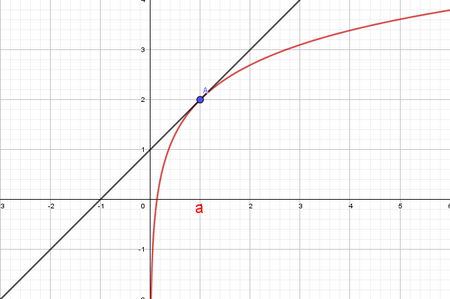
Exemple
II- Dérivabilité à droite – dérivabilité à gauche
2-1/ Définition et propriété
Définition
Soit une fonction définie sur un intervalle de type où
On dit que est dérivable à droite de , s’il existe un réel tel que
Le nombre est appelé le nombre dérivé de la fonction à droite en ,noté
Soit une fonction définie sur un intervalle de type où
On dit que est dérivable à gauche de , s’il existe un réel tel que
Le nombre est appelé le nombre dérivé de la fonction à gauche en , noté
Exemple
II- Dérivabilité à droite – dérivabilité à gauche
2-1/ Définition et propriété
Propriété
Soit une fonction définie sur un intervalle ouvert , et soit
est dérivable en est dérivable à droite et à gauche en et
Exemple
II- Dérivabilité à droite – dérivabilité à gauche
2-2/ Interprétation géométrique
Propriété
Si est dérivable à droite en , alors la courbe admet une demi-tangente à droite du point d’abscisse , d’équation :

Si est dérivable à gauche en , alors la courbe admet une demi-tangente à gauche du point d’abscisse , d’équation :
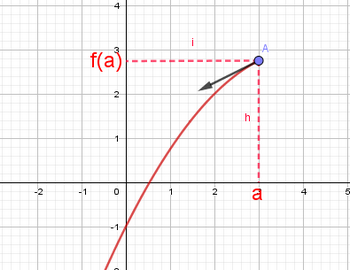
Exemple
II- Dérivabilité à droite – dérivabilité à gauche
2-2/ Interprétation géométrique
Remarques
A- Si dérivable à droite et à gauche en , et
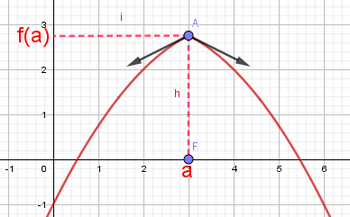
B- Si , alors admet une demi-tangente verticale à droite du point d’abscisse .
 |
 |
C- Si , alors admet une demi-tangente verticale à gauche du point d’abscisse .
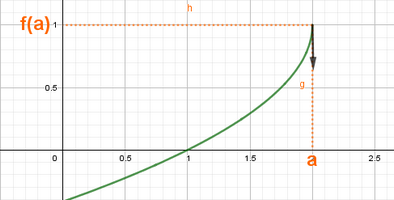 |
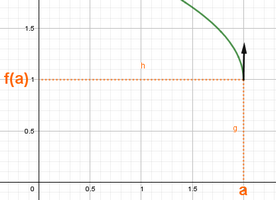 |
III- Dérivabilité d’une fonction sur un intervalle
3-1/ Définition
On dit que est dérivable sur l’intervalle ouvert si est dérivable en tout point de l’intervalle .
On dit que est dérivable sur l’intervalle fermé si est dérivable sur l’intervalle , et dérivable à droite en et à gauche en .
III- Dérivabilité d’une fonction sur un intervalle
3-2/ Propriété
Toute fonction polynomiale est dérivable sur .
Toute fonction rationnelle est dérivable sur son domaine de définition.
La fonction est dérivable sur .
Exemple
III- Dérivabilité d’une fonction sur un intervalle
3-3/ Tableau des dérivées usuelles

Exemple
III- Dérivabilité d’une fonction sur un intervalle
3-4/ Opérations sur les fonctions dérivées
Propriété 1
Soient et deux fonctions dérivables sur un intervalle , et soit .
Les fonctions et sont dérivables sur , et on a :
Si ne s’annule pas sur , alors les fonctions et sont dérivables sur , et on a :
Exemple
III- Dérivabilité d’une fonction sur un intervalle
3-4/ Opérations sur les fonctions dérivées
Propriété 2
Soit une fonction dérivable sur un intervalle , et soit , on a :
La fonction est dérivable sur , et on a :
Si est strictement positive sur , alors la fonction est dérivable sur , et on a :
Exemple
III- Dérivabilité d’une fonction sur un intervalle
3-4/ Opérations sur les fonctions dérivées
Propriété 3 (Dérivée de la fonction Réciproque)
Soit une fonction continue et strictement monotone sur un intervalle de , et soit
Si est dérivable en et , alors est dérivable en et
Corollaire
Soit une fonction continue et strictement monotone sur un intervalle de
Si est dérivable sur telle que la fonction ne s’annule pas sur , alors la fonction est dérivable sur .
De plus pour tout on a:
Exemple
IV- Applications de la dérivation
4-1/ Variations d’une fonction
Propriété 1
Soit une fonction dérivable sur un intervalle , alors:
est croissante sur
est strictement croissante sur
est décroissante sur
est strictement décroissante sur
est constante sur
Exemple
IV- Applications de la dérivation
4-1/ Variations d’une fonction
Propriété 2
Soit une fonction dérivable sur un intervalle , alors :
Si est positive sur , et ne s’annule qu’en un nombre fini des points, alors est strictement croissante sur .
Si est négative sur , et ne s’annule qu’en un nombre fini des points, alors est strictement décroissante sur .
Exemple
IV- Applications de la dérivation
4-2/ Valeur minimale et maximale
Propriété 1
Soit une fonction dérivable sur un intervalle ouvert , et soit
Si admet un extremum en un point , alors
 |
 |
| admet un maximum en | admet un minimum en |
Propriété 2
Soit une fonction dérivable sur un intervalle ouvert , et soit
Si s’annule en en changeant de signe, alors admet un extremum en .
Exemple
IV- Applications de la dérivation
4-3/ Étude de la concavité d’une courbe
Définition
Soit une fonction deux fois dérivable sur un intervalle , alors:
Pour que la courbe de soit convexe sur ,il faut et il suffit que
Pour que la courbe de soit concave sur ,il faut et il suffit que
Pour que le point soit un point d'inflexion de la courbe , il faut et il suffit que la dérivée seconde s'annule en , et change de signe de part et d'autre de .
Exemple
V- Exercices
5-1/ Exercice 1
Étudier la dérivabilité de la fonction en dans chacun des cas suivants :
V- Exercices
5-2/ Exercice 2
Pour chacun des cas suivants indiquer l’ensemble de dérivabilité de la fonction puis déterminer :
V- Exercices
5-3/ Exercice 3
Soit la fonction numérique définie par :
- Étudier les variations de la fonction
Soit la restriction de sur
- Montrer que admet une fonction réciproque définie sur un intervalle à déterminer
- Montrer que l’équation admet une unique solution et que
- Montrer que :
V- Exercices
5-4/ Exercice 4
En utilisant la fonction dérivée, étudier les variations de la fonction dans chacun des cas suivants :
V- Exercices
5-5/ Exercice 5
Soit la fonction définie par :
- Déterminer
- Déterminer la fonction dérivée de la fonction .
- Donner le tableau de variations de la fonction .
- Déterminer les extremums de la fonction .
- Etudier la concavité de .
V- Exercices
5-6/ Exercice 6
Soit la fonction définie par :
- Montrer que est dérivable sur puis calculer .
- Montrer que admet une fonction réciproque définie sur un intervalle que l'on précisera.
- Calculer , montrer que est dérivable en , puis calculer .
- Calculer en fonction de .


