Physique et Chimie : 2ème Année Bac
Séance 1 (Les ondes mécaniques progressives)
Professeur : Mr El GOUFIFA Jihad
Sommaire
I- Définitions
1-1/ Onde mécanique
1-2/ Milieu matériel élastique
II- Types d’ondes
2-1/ Onde transversale
2-2/ Onde longitudinale
III- L’onde mécanique progressive
IV- L’onde sonore
V- Propriétés des ondes mécaniques
5-1/ Dimension d’onde
5-2/ Superposition d’ondes
VI- Vitesse de propagation d’une onde
6-1/ Définition
6-2/ Facteurs influençant la célérité de propagation
VII- Notion de retard
VIII- Exercices
8-1/ Exercice 1
8-2/ Exercice 2
8-3/ Exercice 3
8-4/ Exercice 4
I- Définitions
1-1/ Onde mécanique
C’est le phénomène de propagation d’une perturbation dans un milieu matériel sans transport de la matière, mais avec le transport de l’énergie.
1-2/ Milieu matériel élastique
(compressible et expansible) S’il est capable de reprendre sa forme initiale après avoir subit le passage d’une onde.
II- Types d’ondes
2-1/ Onde transversale
Une onde est dite transversale si la direction de la perturbation du milieu est perpendiculaire à la direction de propagation d’onde.
Exemple
L’onde le long d’une corde ou à la surface de l’eau.
2-2/ Onde longitudinale
Une onde est dite longitudinale si la direction de la perturbation du milieu est alignée avec la direction de la propagation de l’onde.
Exemple
L’onde le long d’un ressort ou l’onde sonore.
III- L’onde mécanique progressive
L’onde mécanique progressive est une succession entretenue des signaux mécaniques qui se propagent dans un milieu supposé infini.
Nous pouvons générer une onde mécanique progressive par la vibration entretenue d’une source.
Exemple
En faisant tomber l'eau successivement à la surface libre d'une eau, goutte par goutte, à l'aide d'un robinet on obtient une onde mécanique progressive.

IV- L’onde sonore
4-1/ Expériences
|
|
|
4-2/ Observations
Expérience 1
On observe l’absence de son Après le vidage de l’air, on conclut que le son ne se propage pas dans le vide mais il nécessite un milieu matériel pour se propager.
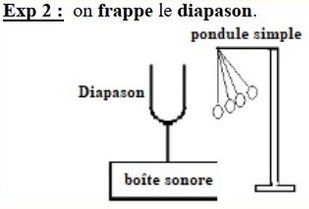
Expérience 2
Lorsqu’on frappe le diapason, la balle se déplace horizontalement, ce qui indique que la direction de perturbation et celle de propagation sont alignées, donc le son est une onde longitudinale.
4-3/ Conclusion
Le son est une onde mécanique progressive longitudinale se propage dans les milieux matériels (solide et liquide et gaz) et ne se propage pas dans le vide, et il se propage grâce à une compression et une dilatation du milieu de propagation.

V- Propriétés des ondes mécaniques
5-1/ Dimension d’onde
Une onde mécanique se propage à partir de la source dans toutes les directions qui lui sont offertes :
- L’onde à une dimension : se propage selon un axe depuis sa source, à titre d’exemple le ressort.
- L’onde à deux dimensions : se propage selon deux axes depuis sa source, comme l’onde à la surface de l’eau.
- L’onde à trois dimensions : se propage selon trois axes (L’espace (x, y, z)) depuis sa source, par exemple l’onde sonore.
5-2/ Superposition d’ondes
Lorsque plusieurs ondes de propagent dans la même région, elles se propagent en conservant leur intégrité, c-à-d leurs amplitudes s’ajoutent algébriquement, puis elles s’éloignent sans être altérées.
VI- Vitesse de propagation d’une onde
6-1/ Définition
La vitesse de propagation d'une onde (nommée célérité) est égale à la distance parcourue au temps mis à la parcourir.
Elle est donné par la relation suivante :
est la célérité de l’onde (m/s)
est la distance parcourue (m)
est la durée du parcours (s)
6-2/ Facteurs influençant la célérité de propagation
Pour un milieu homogène, la célérité d’une onde est constante et indépendante de la forme de la perturbation. Tandis qu’elle dépend de la nature du milieu : son élasticité, son inertie et de sa température.
Influence de l’élasticité du milieu
La célérité d’une onde augmente avec l’élasticité du milieu de propagation.
Exemple: La célérité d’une onde le long d’une corde augmente avec l’augmentation de sa tension.
Influence de l’inertie du milieu
L’inertie d’un milieu ou d’un système représente la résistance que ce milieu ou ce système oppose lorsqu’on cherche à le mettre en mouvement.
La célérité d’une onde dans un milieu dépend de son inertie. Plus l’inertie du milieu est grande et plus la célérité de l’onde se propageant dans ce milieu est faible.
Par exemple, l’inertie d’une corde est représentée par sa masse linéique (masse par unité de longueur).
La célérité d’une onde le long d’une corde est donnée par:
où est la tension de la corde et sa masse linéique.
Pour l’onde sonore, la célérité augmente avec la densité du milieu de propagation:

Pour les gaz, la célérité du son augmente avec la température du milieu.
VII- Notion de retard
Au cours de la propagation d’une onde mécanique non amortie, tous les points du milieu de propagation subissent la même perturbation que la source S mais avec un retard tel que:
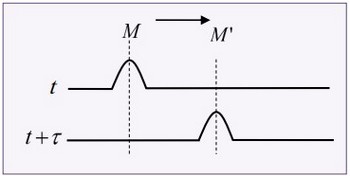
En général : Le retard d’un point M' par rapport un point M est donné par:
La relation entre l’élongation d'un point M du milieu de propagation et celle de la source est : avec :
VIII- Exercices
8-1/ Exercice 1
La figure ci-dessous représente la propagation d’une onde le long d’une corde élastique (AB), sa longueur AB=10m à deux instants et
- Est ce que la perturbation conserve sa forme lors de la propagation ?
- Cette onde est-elle longitudinale ou transversale ? Justifier.
- Calculer la célérité de la propagation de l’onde le long de la corde.
- Déterminer la durée de la perturbation d’un point de la corde.
- Dessiner l’aspect de la corde à l’instant
VIII- Exercices
8-2/ Exercice 2
La figure ci-dessous représente la propagation d'une onde le long d’une corde :
Elle représente l’aspect de la corde à l’instant .
Sachant que la déformation commence à partir d’une source à l’instant :
- Définir une onde mécanique progressive.
- Quelle est la nature de de l’onde ? quelle est sa dimension ?
- Déterminer à l’instant t les points qui se dirigeront vers le bas ainsi que ceux se dirigeront vers le haut.
- Calculer la célérité de la propagation de l’onde le long de la corde.
- À quel instant s’arrête le point M (position du début de la propagation) ?
- Représenter graphiquement l’aspect de la corde à l’instant .
- Déterminer parmi les propositions suivantes la / les relation (s) entre l’élongation du point M et celle de la source S :
VIII- Exercices
8-3/ Exercice 3
Pour mesurer la propagation des ondes sonores dans l’air on réalise le montage expérimental ci-dessous :
La distance entre les deux microphones et est d=1,70 m . La courbe ci-dessous représente la variation de la tension aux bornes de chaque microphone.
Donnée :
- La sensibilité horizontale :
- Température d’air :
- Célérité de la propagation du son dans l’eau
- Est que le son est une onde longitudinale ou transversale ?
- Déterminer la valeur du retard temporel entre les microphones et .
- Déduire la valeur de la célérité de la propagation des ondes sonores dans l’air.
- Déterminer la valeur du retard temporel quand on déplace le microphone vers la droite à partir de sa position initiale de
- Comparer et . Que peut-t-on déduire ?
VIII- Exercices
8-4/ Exercice 4
La relation donne la vitesse de propagation d’un signal transversal le long d’une corde tendue, dont est la tension de la corde et sa masse linéaire.
- Calculer la vitesse de propagation d’un signal le long d’une corde de longueur et de masse si sa tension est .
- Quelle est la durée que met le signal pour parcourir la corde toute entière ?
- Comment cette vitesse change si nous utilisons la même corde attachée avec une force de 4 fois la force précédente.
- Nous tendons la corde par une masse marquée :

- Calculer la célérité de la propagation de l’onde le long de la corde.
- on donne :
Nous considérons que les dimensions de la poulie sont négligées et