Séance 29 - Les intérêts simples (Cours)

Sommaire

I- Généralités

1-1/ Notion d'intérêt

1-2/ Formule fondamentale des intérêts simples

1-3/ Calcul des différents éléments de la formule

1-4/ Calcul de l'intérêt global de plusieurs capitaux

II- Valeur acquise par un capital

2-1/ Définition

2-2/ Formule de la valeur acquise

2-3/ Calcul des différents éléments de la formule de la valeur acquise

I- Généralités

1-1/ Notion d'intérêt

Une banque prête à un commerçant (une entreprise) une somme d’argent pendant une durée déterminée.

Le commerçant qui emprunte la somme (capital) paie un loyer, appelé intérêt. La banque (le prêteur) place son capital qui lui rapporte intérêt.

Lorsque les intérêts sont calculés sur une période où ils ne se cumulent pas à la somme de départ pour produire d’autres intérêts, on dit que le prêt est fait en intérêts simples.

• Lorsque l'intérêt est versé en fin de période, il est dit post-compté (ou à terme échu).
• Lorsque l'intérêt est versé en début de période, il est dit précompté (ou payé d’avance).

I- Généralités

1-2/ Formule fondamentale des intérêts simples

Durée de placement exprimée en années

Le montant des intérêts dépend :

• du capital prêté ;
• de la durée du prêt ;
• du taux d'intérêt pratiqué (exprimé en pourcentage).

Si nous désignons par :

• (C) le montant du capital prêté ;
• (n) la durée du prêt (ou placement) ;
• (t) le taux de placement pour 100 DH et pour un an.
• (I) le montant des intérêts.

L'intérêt (I) sera donné par la formule :

$I=\frac{C\times T\times n}{100}$

I- Généralités

1-2/ Formule fondamentale des intérêts simples

Durée de placement exprimée en mois

La durée n d'un placement peut être exprimée en mois. Elle correspond alors à $\frac{n}{12}$ (l’année est diviser en 12 mois).

La formule de calcul de l'intérêt s'écrit alors ainsi :

$I=\frac{C\times T\times n}{1200}$

I- Généralités

1-2/ Formule fondamentale des intérêts simples

Durée de placement exprimée en jours

La durée n d’un placement peut aussi être exprimée en jours. Elle correspond alors à $\frac{n}{360}$.

L'usage étant de retenir l'année commerciale de 360 jours.

La formule générale prend alors la forme :

$I=\frac{C\times T\times n}{36 000}$

I- Généralités

1-3/ Calcul des différents éléments de la formule

La formule générale de calcul des intérêts simples met enjeu les quatre éléments : C, t, n, I, qui nécessitent la résolution de quatre problèmes différents.

Trois de ces éléments étant connus, le problème consiste à calculer le quatrième.

Ainsi, lorsque la durée de placement est exprimée, par exemple en jours, nous aurons :

$$\begin{gathered} I=\frac{C\times t\times n}{36 000} ; C=\frac{36 000I}{t\times n} \\ t=\frac{36 000I}{C\times n} ; n=\frac{36 000I}{C\times t} \end{gathered}$$

I- Généralités

1-4/ Calcul de l'intérêt global de plusieurs capitaux

La méthode des nombres et des diviseurs fixes est à retenir, surtout lorsque l'on doit calculer l'intérêt global procuré par plusieurs capitaux placés tous au même taux.

Exemple

Calculer au taux unique de 9%, l'intérêt global fourni par les capitaux suivants :

• 2 500,00 DH pendant 24 jours.
• 1 800,00 DH pendant 36 jours.
• 1 200,00 DH pendant 48 jours.

II- Valeur acquise par un capital

2-1/ Définition

On appelle valeur acquise par un capital placé, le résultat de l'addition à ce capital de l’intérêt qu'il a produit.

Exemple

La valeur acquise par un capital de 15 000,00 DH, placé à 10% pendant 60 jours est égale :

$C+\frac{C\times t\times n}{36 000}=15 000+\frac{15 000\times 10\times 60}{36 000}=15 250 DH$

II- Valeur acquise par un capital

2-2/ Formule de la valeur acquise

Soit C dirhams, un capital placé pendant n jours au taux t%.

Les intérêts produits sont égaux à $I=\frac{C\times n}{D}$.

Si l'on désigne par C' la valeur acquise, on peut écrire successivement :

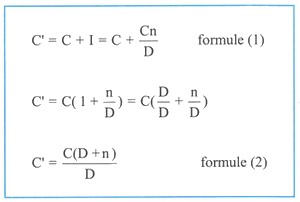
Cette égalité exprime une relation entre les quatre éléments C', C, D et n.

Connaissant trois d'entre eux, on peut calculer le quatrième.

D'où quatre nouveaux problèmes analogues aux précédents, que l'on résout en particulier par la méthode algébrique.

II- Valeur acquise par un capital

2-3/ Calcul des différents éléments de la formule de la valeur acquise

On utilise la formule (1) que l'on retrouve facilement.

Exemple

1. Quelle est la valeur acquise par un capital de 4 500,00 DH placé pendant 48 jours à 9% ?