
Mathématiques : 1Bac S.Exp – STE – STM
Séance 8 (Les limites d’une fonction numérique)
Professeur : Mr ETTOUHAMY Abdelhak
Sommaire
I- Limite infinie d’une fonction en +∞ ou en -∞
II- Limite finie d’une fonction en +∞ et en -∞
III- Limite finie et limite infinie d’une fonction en un point
3-1/ Limite finie d’une fonction en un point
3-2/ Limite infinie d’une fonction en un point
IV- Limite à droite et limite à gauche d’une fonction en un point
V- Opérations sur les limites
5-1/ Limite d’une somme
5-2/ Limite d’un produit
5-3/ Limite de l’inverse
5-4/ Limite d’un quotient
VI- Limites de fonctions particulières
6-1/ Limite d’une fonction polynôme - Limite d’une fonction rationnelle
6-2/ Limites des fonctions irrationnelles
6-3/ Limites des fonctions trigonométriques
VII- Théorème de comparaison
IIX- Exercices
8-1/ Exercice 1
8-2/ Exercice 2
8-3/ Exercice 3
8-4/ Exercice 4
8-5/ Exercice 5
8-6/ Exercice 6
I- Limite infinie d’une fonction en +∞ ou en -∞
Activité
Considérons la fonction f définie par : f(x)=x2
- Représenter graphiquement la fonction f dans un repère orthonormé (O;→i;→j)
- Compléter le tableau suivant :
| x | -1020 | -1010 | -10 | 10 | 1010 | 1020 |
| f(x) |
- Que remarquer pour les valeurs de f(x) quand x prend des valeurs positives de plus en plus grands (c-à-d quand x tend vers +∞).
- Que remarquer pour les valeurs de f(x) quand x prend des valeurs négatives de plus en plus (c-à-d quand x tend vers -∞).
- Conjecturer les limites suivantes : limx→+∞x3 et limx→-∞x3
I- Limite infinie d’une fonction en +∞ ou en -∞
Remarque
Soit f une fonction numérique définie sur un intervalle de la forme : [a,+∞[
Si tend vers quand tend vers , on écrit : ou
On peut exprimer aussi par des phrases les symboles suivantes :
- (Il faut que ).
I- Limite infinie d’une fonction en ou en
Limites usuelles
On admet les limites suivantes :
II- Limite finie d’une fonction en ou en
Activité
Considérons la fonction définie par :
- Représenter graphiquement la fonction dans un repère orthonormé
- Compléter le tableau suivant :
- Que remarquer pour les valeurs de quand prend des valeurs positives de plus en plus grands (c-à-d quand tend vers ).
- Que remarquer pour les valeurs de quand prend des valeurs négatives de plus en plus (c-à-d quand tend vers ).
- Conjecturer les limites suivantes : et
II- Limite finie d’une fonction en ou en
Remarque
Soit une fonction numérique définie sur un intervalle de la forme : , et soit
Si tend vers le nombre quand tend vers , on écrit : ou
Soit une fonction numérique définie sur un intervalle de la forme : , et soit
Si tend vers le nombre quand tend vers , on écrit : ou
II- Limite finie d’une fonction en ou en
Interprétation géométrique
La courbe se rapproche de la droite d’équation au voisinage de .

II- Limite finie d’une fonction en ou en
Propriété 1
et
En général : et
On a aussi :
II- Limite finie d’une fonction en ou en
Propriété 2
Soit une fonction numérique et .
- Si f admet en (ou en ) une limite, alors cette limite est unique.
-
-
III- Limite finie et limite infinie d’une fonction en un point
3-1/ Limite finie d’une fonction en un point
Définition
Soit et et soit une fonction définie sur un intervalle de la forme où , ou sur un intervalle de la forme .
Si tend vers quand tend vers alors on note :
Soit une fonction numérique et .
- Si f admet en (ou en ) une limite, alors cette limite est unique.
-
-
III- Limite finie et limite infinie d’une fonction en un point
3-1/ Limite finie d’une fonction en un point
Propriété
Si admet une limite finie en alors cette limite est unique.
III- Limite finie et limite infinie d’une fonction en un point
3-2/ Limite infinie d’une fonction en un point
Définition
Soit une fonction définie sur un intervalle de la forme .
Si tend vers quand tend vers alors on note :
On définie de la même façon :
III- Limite finie et limite infinie d’une fonction en un point
3-2/ Limite infinie d’une fonction en un point
Exercice
- Calculer les limites suivantes :
III- Limite IV- Limite à droite et limite à gauche d’une fonction en un pointet limite infinie d’une fonction en un point
Activité
Soit la fonction définie par :
- Déterminer .
- Construire la courbe de la fonction .
- À partir de la représentation graphique, que-remarque-t-on pour les valeurs de quand tend vers et
- Que-remarque-t-on pour les valeurs de quand tend vers et
III- Limite IV- Limite à droite et limite à gauche d’une fonction en un pointet limite infinie d’une fonction en un point
Théorème
Soit une fonction définie sur un intervalle de centre , on a :
V- Opérations sur les limites
5-1/ Limite d’une somme

V- Opérations sur les limites
5-2/ Limite d’un produit

V- Opérations sur les limites
5-3/ Limite de l’inverse
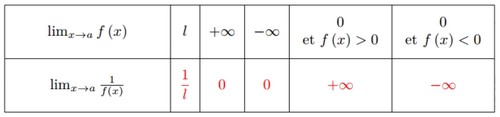
V- Opérations sur les limites
5-4/ Limite d’un quotient

VI- Limites de fonctions particulières
6-1/ Limite d’une fonction polynôme - Limite d’une fonction rationnelle
Propriété
Soient et deux fonctions polynômes et , alors on a :
-
- Si , alors :
- Si et sont des termes de plus haut degré de et respectivement ( et ), alors :
et
VI- Limites de fonctions particulières
6-2/ Limites des fonctions irrationnelles
Propriété
Soit une fonction numérique définie sur un intervalle de la forme , avec
- Si et , alors :
- Si , alors :
VI- Limites de fonctions particulières
6-3/ Limites des fonctions trigonométriques
Propriété
VII- Théorème de comparaison
Théorème
Soit un intervalle de la forme et et soient , et des fonctions définies sur :
IIX- Exercices
8-1/ Exercice 1
- Déterminer les limites suivantes :
IIX- Exercices
8-2/ Exercice 2
Soit la fonction définie par :
- Déterminer .
- Calculer les limites de aux bornes de .
Soit la fonction définie par :
- Déterminer et
- Est que la fonction admet une limite en ?
IIX- Exercices
8-3/ Exercice 3
- Calculer les limites suivantes :
IIX- Exercices
8-4/ Exercice 4
- Calculer les limites suivantes :
IIX- Exercices
8-5/ Exercice 5
- Calculer les limites suivantes :
IIX- Exercices
8-6/ Exercice 6
- Calculer les limites suivantes :


