
Physique et Chimie : Tronc Commun
Séance 11 (Équilibre d'un solide en rotation autour d'un axe fixe)
Professeur : Mr EL GOUFIFA Jihad
Sommaire
I- Effet d’une force sur la rotation d’un solide
II- Moment d'une force par rapport à un axe
2-1/ Définition
2-2/ Moment : grandeur algébrique
III- Équilibre d’un solide en rotation autour d’un axe fixe
3-1/ Théorème des moments
3-2/ Conditions d’équilibre
IV- Moment d’un couple de forces
4-1/ Définition d'un couple de forces
4-2/ Moment d'un couple de forces
4-3/ Couple et sens de rotation
4-4/ Moment du couple de torsion
4-5/ Méthode de résolution d'un problème à moments
V- Exercices
5-1/ Exercice 1
5-2/ Exercice 2
5-3/ Exercice 3
5-4/ Exercice 4
I- Effet d’une force sur la rotation d’un solide
On exerce sur une porte ouverte 3 forces différentes :
- La force ne met pas la porte en mouvement de rotation car a une direction parallèle à l’axe de rotation.
- La force ne met pas non plus la porte en mouvement car la direction de coupe l’axe de rotation.
- La force provoque une rotation de la porte par ce que la direction de et l’axe de rotation ni parallèle ni concourante

Nous admettrons que : Lorsque la droite d’action de la force exercée sur un solide et son axe de rotation sont concourante ou parallèles, l’effet de rotation est nul.
II- Moment d'une force par rapport à un axe
2-1/ Définition
Le moment d'une force par rapport à un axe traduit son efficacité à produire un effet de rotation du solide autour de cet axe.
L'intensité du moment par rapport à un axe d'une force orthogonale à cet axe est le produit de l'intensité de cette force par la distance séparant la droite d'action de la force et l'axe :

II- Moment d'une force par rapport à un axe
2-2/ Moment : grandeur algébrique
Afin de distinguer les deux possibilités de sens de rotation, nous évaluerons algébriquement le moment d une force par rapport à l'axe par l'une des expressions suivantes :
- Lorsque tend à faire tourner le solide dans le sens positif choisi :
 |
- Lorsque tend à faire tourner le solide dans le sens contraire au sens positif choisi :
 |
III- Équilibre d’un solide en rotation autour d’un axe fixe
3-1/ Théorème des moments
Lorsqu un solide, mobile autour d un axe fixe est en équilibre, la somme algébrique des moments de toutes les forces extérieures appliquées à ce solide par rapport à cet axe est nulle :
III- Équilibre d’un solide en rotation autour d’un axe fixe
3-2/ Conditions d’équilibre
Lorsque un solide est en équilibre, deux conditions doivent être satisfaites :
- Immobilité du centre de gravité :
- Absence de rotation autour de l'axe :
IV- Moment d’un couple de forces
4-1/ Définition d'un couple de forces
Un couple de force est un système de deux forces parallèles, de sens contraires, de même intensité et n'ayant pas la même droite support (lignes d′action différentes).
Exemples
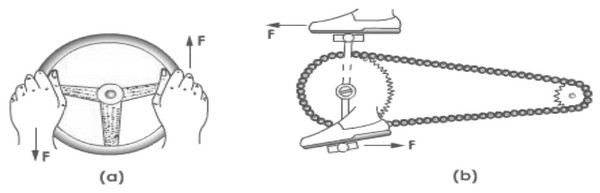
IV- Moment d’un couple de forces
4-2/ Moment d'un couple de forces

Le moment d'un couple de force ne dépend pas de la position de l'axe de rotation mais seulement de la distante des deux lignes d'action.
IV- Moment d’un couple de forces
4-3/ Couple et sens de rotation
Un couple tend à faire tourner un solide dans un sens donné.
Le moment d’un couple est une grandeur algébrique dont le signe dépend du sens de rotation choisi.
- Un couple qui tend à faire tourner le solide dans le sens positif choisi, a un moment positif : le moment est dit moteur
- Un couple qui tend à faire tourner le solide dans le sens contraire du sens positif choisi, a un moment négatif : le moment est dit résistant.
IV- Moment d’un couple de forces
4-4/ Moment du couple de torsion
Un pendule de torsion est un solide suspendu à un fil vertical, le centre de masse étant sur l'axe du fil, l'autre extrémité du fil étant maintenue fixe dans un support.
Quand le solide tourne autour de l'axe du fil, celui-ci réagit à la torsion en exerçant des forces de rappel équivalentes à un couple dont le moment par rapport à l'axe est proportionnel à l'angle de torsion en (rad) :
La constante dite constante de torsion dépend de la longueur et du diamètre du fil (supposé cylindrique) et de la nature du matériau constituant le fil, son unité est
IV- Moment d’un couple de forces
4-5/ Méthode de résolution d'un problème à moments
Pour résoudre un problème faisant intervenir des forces qui agissent sur un solide mobile autour d'un axe, nous allons systématiquement appliquer la procédure suivante :
- Indiquer le système étudié.
- Faire le bilan des forces.
- Déterminer l'axe de rotation et fixer un sens positif de rotation.
- Exprimer le moment des différentes forces et indiquer s'il est positif ou négatif.
- Appliquez les conditions générales d’équilibre.
V- Exercices
5-1/ Exercice 1
Une poulie différentielle de masse négligeable, à deux gorges de rayons respectifs et tel que susceptible de tourner autour d’un axe fixe horizontal passant par son centre .
Un fil de masse négligeable enroulé sur la gorge de rayon , supporte un objet de masse .
On met la poulie en équilibre par un fil enroulé sur l’autre gorge est tendu par la force incliné de par rapport à l’horizontale.

- Faire le bilan de toutes les forces qui s’exercent sur la poulie en équilibre.
- Écrire l’expression de moment de chaque force par rapport à l’axe de rotation .
- En appliquant le théorème des moments, déterminer l’intensité pour réaliser l’équilibre.
- Déterminer les caractéristiques de la réaction de l’axe de rotation.
On donne : .
V- Exercices
5-2/ Exercice 2
Un mobile est constitué de 3 poulies solidaires entre elles pouvant tourner autour du même axe.
On attache à chaque poulie un fil et une masse.

- Le solide est il en équilibre ?
- S'il ne l'est pas, dans quel sens tourne t-il ? 1 ou 2 ? Pourquoi ?
- Par quelle masse devrait-on remplacer pour qu'il soit en équilibre ?
- Si était toujours égale à , à quelle distance de l'axe devrait-on attacher ?
V- Exercices
5-3/ Exercice 3
Une pédale d’accélérateur de poids négligeable de longueur tourne autour d’un axe fixe horizontale passant par .
On exercice une force à l’extrémité A de valeur , la pédale est en équilibre quand le ressort fixé en son milieu prend une direction qui lui est perpendiculaire, la pédale fait un angle avec l’horizontale à l’équilibre.

- Faire inventaire les forces exercent sur la pédale.
- En appliquant le théorème des moments, déterminer l’expression de la valeur de tension de ressort en fonction de et . Calculer-la.
- Déduire la constante de raideur de ressort sachant que l’élongation soit .
- Déterminer les caractéristiques de la réaction de l’axe de rotation sur la pédale.
V- Exercices
5-4/ Exercice 4
Une console numérotée 1, mobile autour d’un axe , supporte une charge appliquée en par l’intermédiaire du câble 2.
Un autre câble numéroté 3, fixe dans le mur 4, maintient la console en position horizontale.
On supposera que le poids de la console et le poids des câbles sont négligeables.
On se propose de déterminer les actions qui s’exercent sur la console .

- Faire le bilan des actions s'exerçant sur la console .
- Tracer la direction de ces forces sur la figure (le point d’intersection de ces 3 droites est ).
- Déterminer une des intensités manquantes avec le théorème des moments.
- Sur un deuxième graphique, construisez la dynamique (ligne polygonale) des forces (Échelle : ), et déterminer l’intensité de la 3ème force.
- Déterminer les caractéristiques de ces forces.


