Séance 1 - La gravitation universelle

Sommaire

I- Introduction

II- Échelle des longueurs

2-1/ Écriture Scientifique

2-2/ Ordre de grandeur

III- Loi de la gravitation

3-1/ Énoncé de la loi de gravitation

3-2/ Formulation mathématique

IV- Champ de gravitation

4-1/ Notion de champ gravitationnel

4-2/ Attraction gravitationnelle entre la terre et un corps

V- Poids du corps

5-1/ Définition

5-2/ Caractéristiques du poids d’un corps

5-3/ La pesanteur

VI- Exercices

6-1/ Exercice 1

6-2/ Exercice 2

6-3/ Exercice 3

6-4/ Exercice 4

I- Introduction

Toutes les planètes du système solaire gravitent autour du soleil.

• Comment peut-on expliquer la cohésion de ce système solaire ?
• Pourquoi la lune tourne-t-elle autour de la terre ?
• Pourquoi une pomme tombe-t-elle d’arbre vers le bas ?

II- Échelle des longueurs

2-1/ Écriture Scientifique

L’écriture scientifique d’un nombre s’écrit sous la forme :

$\overline{) N=a.{10}^n }$

• $a$ est un nombre décimal $\left(1\le a<10\right)$
• $n$ est un nombre entier relatif

II- Échelle des longueurs

2-2/ Ordre de grandeur

L’ordre de grandeur d’un nombre est la puissance de 10 la plus proche de ce nombre.

Pour trouver l’ordre de grandeur d’un nombre on doit l’écrire en notation scientifique qui se compose d’un nombre à multiplier par ${10}^n$, puis on applique la règle suivante :

• Si $a<5$ alors l'ordre de grandeur du nombre est ${10}^n$.
• Si $a>5$ alors l'ordre de grandeur est ${10}^{n+1}$.

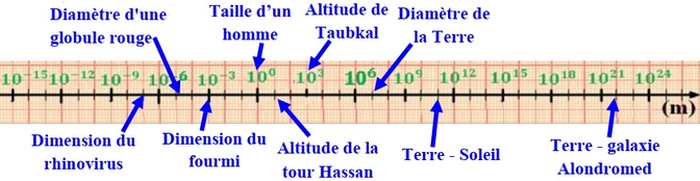
Connaître l’ordre de grandeur d’une longueur permet de la situer sur l’échelle des longueurs qui composent notre univers, et de la comparer aux autres longueurs.

On peut ainsi mémoriser facilement certaines tailles ou distances caractéristiques (Exemple : l’ordre de grandeur du diamètre atomique est ${10}^{-10}m$).

Estimer l’ordre de grandeur d’une longueur permet également de vérifier rapidement un calcul.

III- Loi de la gravitation

3-1/ Énoncé de la loi de gravitation

Newton énonça la loi de gravitation universelle en 1687.

D’après cette loi, deux corps, à couse de leurs masse, exercent l’un sur l’autre une force gravitationnelle qui est attractive.

Deux corps A et B, assimilables à des points, s’attirent mutuellement, l’attraction qu’ils exercent l’un sur l’autre est:

• Proportionnelle a leurs masse m(A) et m(B)
• Inversement proportionnelle au carré de la distance d entre les deux points.

III- Loi de la gravitation

3-2/ Formulation mathématique

Deux corps ponctuels $A$ et $B$, de masses respectivement $m_A$ et $m_B$, séparés par une distance $d=AB$, exercent l’un sur l’autre des forces d’interactions gravitationnelles attractives ${\overrightarrow{F}}_{\raisebox{1ex}{$A$}\!\left/ \!\raisebox{-1ex}{$B$}\right.}$ et ${\overrightarrow{F}}_{\raisebox{1ex}{$B$}\!\left/ \!\raisebox{-1ex}{$A$}\right.}$ ayant :

• La même droite d’action $\left(AB\right)$
• Des sens opposés (vers le corps qui exerce la force)
• La même intensité :

$\overline{) F_{\raisebox{1ex}{$A$}\!\left/ \!\raisebox{-1ex}{$B$}\right.}=F_{\raisebox{1ex}{$B$}\!\left/ \!\raisebox{-1ex}{$A$}\right.}=G\frac{m_A\times m_B}{d^2} }$

G : Constante de gravitation universelle

$G=6,67\times {10}^{-11}N.m^2.K{g}^{-2}$

IV- Champ de gravitation

4-1/ Notion de champ gravitationnel

Pour interpréter l’interaction gravitationnelle, on peut stipuler que tout objet (A) (de masse M et placé en une origine spatiale O) crée autour de lui un champ gravitationnel attractif.

En un point P (hors de l’objet (A)), si un second objet de masse m y est placé, alors il sera soumis à la force de gravitation exercée par (A).

Nous supposerons que le corps situé en P ne modifie pas le champ de gravitation auquel il est soumis.

IV- Champ de gravitation

4-2/ Attraction gravitationnelle entre la terre et un corps

Tout corps A, de centre C et de masse m, placé au voisinage de la Terre subit une force gravitationnelle de la part de la Terre.

Le centre de la Terre est noté T, sa masse $m_T$ et son rayon $R_T$ :

L’attraction exercé par la Terre sur le corps A est modélisée par la force caractérisée par :

• Point d’application : C
• Direction : la droite (TC), elle passe par le centre de la Terre. C’est la verticale du lieu.
• Sens : de C vers T. La force est orientée vers le bas.
• Valeur de la force : $F_{\raisebox{1ex}{$Terre$}\!\left/ \!\raisebox{-1ex}{$A$}\right.}=G\frac{m\times m_T}{d^2}$

Si le corps est au voisinage de la Terre ou à la surface de la Terre on considère que $d\approx R_T$, donc :

$\overline{) F_{\raisebox{1ex}{$Terre$}\!\left/ \!\raisebox{-1ex}{$A$}\right.}=G\frac{m\times m_T}{{R_T}^2}=m\left(G\frac{m_T}{{R_T}^2}\right) }$

V- Poids du corps

5-1/ Définition

Sur terre, par définition, le poids est l’action exercée par la terre sur tout objet se trouvant à proximité de sa surface.

Il ne s’agit que d’un cas particulier de l’interaction de gravitation.

Par extension, on peut aussi parler du poids d’un objet à la surface de tout autre astre.

Par exemple, sur la lune, le poids d’un objet est défini comme étant l’interaction exercée par la lune sur celui-ci lorsqu’il se trouve à proximité de la surface lunaire.

V- Poids du corps

5-2/ Caractéristiques du poids d’un corps

Le poids d’un corps situé au voisinage de la terre (un astre) est l’action à distance que la terre exerce sur lui.

Il a les caractéristiques suivantes :

• Direction ou droite d’action : la verticale du lieu
• Sens : de haut en bas
• Point d’application : le centre de gravité de corps
• Valeur : est calculé par la relation suivante : $P=mg$

$P$ : poids en newtons $\left(N\right)$
$m$ : masse en kilogramme $\left(Kg\right)$
$g$ : intensité de la pesanteur $(N.K{g}^{-1})$

V- Poids du corps

5-3/ La pesanteur

Intensité de la pesanteur à la surface de la terre :

$$\begin{gathered} F_{\raisebox{1ex}{$Terre$}\!\left/ \!\raisebox{-1ex}{$A$}\right.}=m\left(G\frac{m_T}{{R_T}^2}\right)=P=m\times g_0 \\ \Rightarrow g_0=G\frac{m_T}{{R_T}^2} \end{gathered}$$

Intensité de la pesanteur à la hauteur h :

$g_h=G\frac{m_T}{{\left(R_T+h\right)}^2}$

La pesanteur dépend de l’altitude, elle diminue quand l’altitude augmente et varie le long d’un méridien ( i.e. varie selon latitude).

Les tableaux suivants donnent, à titre indicatif, la valeur de g selon la latitude et sur quelques astres :

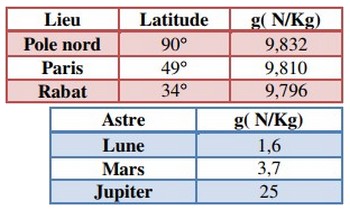
VI- Exercices

6-1/ Exercice 1

1. Compléter le tableau suivant :

2. Représenter ces distances sur l’axe de l’échelle des longueurs.

VI- Exercices

6-2/ Exercice 2

On suppose que la Terre a une masse régulièrement répartie autour de son centre Son rayon est $R=6,38.{10}^{3}km$, sa masse est $M=5,98.{10}^{24}kg$ et la constante de gravitation Universelle est $G=6,67.{10}^{-11}(S.I)$.

1. Déterminer la valeur de la force de gravitation exercée par la Terre sur un ballon de masse $m=0,60kg$ posé sur le sol.

2. Déterminer le poids du même ballon placé dans un lieu où l’intensité de la pesanteur vaut : $g=9,8 N/kg$.

3. Comparer les valeurs des deux forces et conclure.

VI- Exercices

6-3/ Exercice 3

Un corps $\left(S\right)$ de masse $m=50kg$, se trouve à une altitude $h=10km$ par rapport au sol terrestre.

1. Écrire l’expression de la force d’attraction appliquée par la terre sur le corps $\left(S\right)$ à l’altitude $h$ en fonction de $G$, $M_T$, $R_T$ et $h$.

2. Écrire l’expression du poids du corps $\left(S\right)$ à l’altitude $h$ en fonction de sa masse $m$ et l’intensité de pesanteur $g_h$ à l’altitude $h$.

3. En considérant que la force de gravitation est égale au poids du corps, trouver l’expression de $g_h$ à l’altitude $h$ en fonction de $G$, $M_T$, $R_T$ et $h$.

4. En déduire l’expression de l’intensité de pesanteur $g_0$ au sol en fonction de $G$, $M_T$ et $R_T$. Calculer sa valeur.

5. Trouver l’expression de $g_h$ à l’altitude $h$ en fonction de $g_0$, $R_T$ et $h$. Calculer la valeur de $g_h$.

6. Calculer la valeur de l’altitude $h$ ou l’intensité de pesanteur $g_h$ devient égale au quart de sa valeur $g_0$ sur le sol.

VI- Exercices

6-4/ Exercice 4

La Lune est assimilable à un solide dont la masse est régulièrement répartie autour de son centre.

1. Écrire l’expression de la force de gravitation exercée par la Lune de masse $M_L$ sur un objet de masse $m$, situé à la distance $d$ du centre de la Lune.

2. En déduire l’expression littérale de l’intensité de la pesanteur $g_{0L}$ à la surface de la Lune.

Des astronautes (Apollo XVII) ont rapporté $m_R=117kg$ de roches.

3. Déterminer le poids de ces roches :

• a. À la surface de la Lune;
• b. Dans la capsule en orbite autour de la Lune, à l’altitude $h=100km$.

Données

$$\begin{gathered} M_L=7,34.{10}^{22}kg \\ {R}_L=1,74.{10}^{3}km \\ G=6,67.{10}^{-11}SI \end{gathered}$$