Séance 1-2-1 : Limites et continuité - Partie 2 (Cours)

Sommaire

III- Continuité d'une fonction numérique

3-1/ Continuité d'une fonction en un point

3-2/ Continuité à droite - Continuité à gauche

3-3/ Prolongement par continuité en un point

3-4/ Continuité d'une fonction sur un intervalle

3-5/ Opérations sur les fonctions continues

3-6/ Continuité de la composée de deux fonctions

3-7/ Composée d'une fonction continue et d'une fonction admettant une limite

IV- Image d'un intervalle par une fonction continue

4-1/ Image d'un segment par une fonction continue

4-2/ Image d'un intervalle par une fonction continue et strictement monotone

4-3/ Théorème des valeurs intermédiaires

4-4/ Principe de la méthode de dichotomie

III- Continuité d'une fonction numérique

3-1/ Continuité d'une fonction en un point

Définition 2

Soit $f$ une fonction numérique définie sur un intervalle ouvert centré en un point $x_0$.

On dit que la fonction $f$ est continue au point $x_0$ si $\underset{x\to x_0}{\lim }f\left(x\right)=f\left(x_0\right)$

Interprétation Graphique

III- Continuité d'une fonction numérique

3-1/ Continuité d'une fonction en un point

Remarque

si $f$ est définie au point $x_0$ et n'admet pas de limite en $x_0$ ou sa limite est infinie en $x_0$, on dit que $f$ est discontinue au point $x_0$.

$f$ est continue en $x_0$ si :

$\left(\forall \epsilon >0\right)\left(\exists \alpha >0\right) \left(\forall x\in D_f\right) \left(0<\left|x-x_0\right|<\alpha \Rightarrow \left|f\left(x\right)-f\left(x_0\right)\right|<\epsilon \right)$

III- Continuité d'une fonction numérique

3-1/ Continuité d'une fonction en un point

Applications

Soit $f$ la fonction numérique définie par :

$\left\{\begin{array}{l}f\left(x\right)=\frac{-2x^2-x+1}{x+1} \left(x\ne -1\right)\\ f\left(-1\right)=1\end{array}\right.$

1. Étudier la continuité de la fonction $f$ au point $x_0=-1$.

Soit $g$ la fonction numérique définie par :

$\left\{\begin{array}{l}g\left(x\right)=\frac{x+\tan \left(2x\right)}{\sin \left(3x\right)} \left(x\ne 0\right)\\ g\left(0\right)=1\end{array}\right.$

2. La fonction $g$ est-elle continue au point $x_0=0$ ? Justifier la réponse.

III- Continuité d'une fonction numérique

3-2/ Continuité à droite - Continuité à gauche

Définition 3

1- Soit $f$ une fonction définie sur un intervalle de la forme $[x_0,x_0+\alpha [$ où $\alpha \in {\mathrm{ℝ}}^{+}*$.

On dit que $f$ est continue à droite en $x_0$ si $\underset{x\to {x_0}^{+}}{\lim }f\left(x\right)=f\left(x_0\right)$.

2- Soit $f$ une fonction définie sur un intervalle de la forme]x0 - or,x0] où or e R * .

On dit que $f$ est continue à gauche en $x_0$ si $\underset{x\to {x_0}^{-}}{\lim }f\left(x\right)=f\left(x_0\right)$.

III- Continuité d'une fonction numérique

3-2/ Continuité à droite - Continuité à gauche

Proposition 4

Une fonction numérique $f$ est continue au point $x_0$ si et seulement si elle est continue à droite et à gauche au point $x_0$.

En d’autres termes :

($f$ est continue au point $x_0$)$\iff \underset{x\to {x_0}^{+}}{\lim }f\left(x\right)=\underset{x\to {x_0}^{-}}{\lim }f\left(x\right)=f\left(x_0\right)$

III- Continuité d'une fonction numérique

3-2/ Continuité à droite - Continuité à gauche

Applications

Soit $f$ la fonction numérique définie par :

$\left\{\begin{array}{l}f\left(x\right)=\frac{x}{x+1} \left(x\le 0\right)\\ f\left(x\right)=\frac{x^2-x}{x+3} \left(x>0\right)\end{array}\right.$

1. Étudier la continuité de la fonction $f$ en $0$.

Soit $g$ la fonction numérique définie par :

$\left\{\begin{array}{l}g\left(x\right)=x^2+2x \left(x\le 1\right)\\ g\left(x\right)=\frac{a\sin \left(x-1\right)}{x-1} \left(x>1\right)\end{array}\right.$

2. Déterminer la valeur du réel a pour que la fonction $g$ soit continue au point $x_0=1$.

On considère la fonction $h$ définie par :

$\left\{\begin{array}{l}h\left(x\right)=\frac{\left|\sqrt{2}-2\cos x\right|}{4\mathrm{\pi }-\mathrm{x}} \left(x\ne \frac{\mathrm{\pi }}{4}\right)\\ h\left(\frac{\mathrm{\pi }}{4}\right)=\frac{\sqrt{2}}{4}\end{array}\right.$

3. Montrer que la fonction h n’est pas continue au point $x_0=\frac{\mathrm{\pi }}{4}$.

III- Continuité d'une fonction numérique

3-3/ Prolongement par continuité en un point

Définition 4

Soit $f$ une fonction numérique non définie en un point $x_0 \left(x_0\in D_f\right)$ et admettant une limite finie $\mathcal{l}$ au point $x_0 : \underset{x\to x_0}{\lim }f\left(x\right)=\mathcal{l}$.

La fonction $\tilde{f}$ définie sur $D_{\tilde{f}}=D_f\cup \left\{x_0\right\}$ par $\left\{\begin{array}{l}\tilde{f}\left(x\right)=f\left(x\right) \left(x\in D_f\right)\\ \tilde{f}\left(x_0\right)=\mathcal{l}\end{array}\right.$

est continue au point $x_0$, et est appelée le prolongement par continuité de $f$ au point $x_0$.

III- Continuité d'une fonction numérique

3-3/ Prolongement par continuité en un point

Applications

Pour chacun des cas suivants, montrer que la fonction $f$ admet un prolongement par continuité au point $x_0$ puis donner ce prolongement :

$$\begin{gathered} \overline{)1} f\left(x\right)=\frac{x^3-2x^3+3x+6}{x+1} \left(x_0=-1\right) \\ \overline{)2} f\left(x\right)=\frac{x\sin x}{\cos x-1} \left(x_0=0\right) \\ \overline{)3} f\left(x\right)=\frac{\left|x^2+4x\right|-3}{x+3} \left(x_0=-3\right) \\ \overline{)4} f\left(x\right)=\left(x-1\right)\sin \left(\frac{1}{x-1}\right) \left(x_0=1\right) \end{gathered}$$

III- Continuité d'une fonction numérique

3-4/ Continuité d'une fonction sur un intervalle

Définition 5

1- Une fonction $f$ est continue sur un intervalle ouvert $I$ si elle est continue en tout point de $I$.

En particulier : $f$ est continue sur $]a,b[$ si elle est continue en tout point de $]a,b[$.

2- Une fonction $f$ est continue sur $[a,b]$ si elle est continue sur $]a,b[$ et continue à droite en $a$ et à gauche en $b$.

3- Une fonction $f$ est continue sur $[a,b[$ si elle est continue sur $]a,b[$ et continue à droite en $a$.

4- Une fonction $f$ est continue sur $]a,b]$ si elle est continue sur $]a,b[$ et continue à gauche en b.

III- Continuité d'une fonction numérique

3-4/ Continuité d'une fonction sur un intervalle

Application

Soit $f$ la fonction numérique de la variable réelle $x$ définie par : $f\left(x\right)=x-E\left(x\right)$

1. Montrer que la fonction $f$ est continue sur l’intervalle $[1,2[$.

2. Montrer que pour tout $k\in \mathrm{\mathbb{Z}}$, la fonction  est continue sur l'intervalle $[k,k+1[$.

III- Continuité d'une fonction numérique

3-5/ Opérations sur les fonctions continues

Proposition 5

Soit $f$ et $g$ deux fonctions continues sur un intervalle $I$ et $k$ un nombre réel.

Alors :

(1) Les fonctions $f+g$ , $k.f$ et $f.g$ sont continues sur $I$.

(2) Pour tout $n\in \mathrm{\mathbb{N}}*$, la fonction $f^n:x\mapsto {\left(f\left(x\right)\right)}^n$ est continue sur $I$.

(3) Si la fonction $g$ ne s'annule pas sur $I$, alors $\frac{1}{g}$ et $\frac{f}{g}$ sont continues sur $I$.

(4) La fonction $\left|f\right|$ est continue sur $I$.

(5) Si $f$ est positive sur $I$, alors $\sqrt{f}$ est continue sur $I$.

III- Continuité d'une fonction numérique

3-5/ Opérations sur les fonctions continues

Applications

1. Dans chacun des^cas suivants, montrer que la fonction $f$ est continue sur son domaine de définition :

$$\begin{gathered} \overline{)1} f\left(x\right)=\frac{4x+5}{x^2+3}\sin x \\ \overline{)2} f\left(x\right)=\left|2x-3\right|+\frac{x+1}{x^2+x+1} \\ \overline{)3} f\left(x\right)=x^2-\tan x-1 \end{gathered}$$

Soit $g$ la fonction numérique définie par : $g\left(x\right)=\frac{\sqrt{x-2}}{4-x}$

2. Montrer que $g$ est continue sur l’intervalle $[2;4[$.

3. Étudier la continuité de la fonction $x\mapsto xE\left(x\right)$ sur l’intervalle $[0;2]$.

III- Continuité d'une fonction numérique

3-6/ Continuité de la composée de deux fonctions

Proposition 6

Soit $f$ une fonction définie sur un intervalle $I$ et $g$ une fonction définie sur un intervalle $J$ tel que $f\left(I\right)\subset J$, et soit $x_0$ un élément de $I$.

Si $f$ est continue au point $x_0$ et $g$ est continue au point $f\left(x_0\right)$, alors la fonction $g\circ f$ est continue en $x_0$.

Corollaire

Si $f$ est continue sur un intervalle $I$ et $g$ est continue sur un intervalle $J$ tel que $f\left(I\right)\subset J$, alors la fonction $g\circ f$ est continue sur l'intervalle $I$.

III- Continuité d'une fonction numérique

3-6/ Continuité de la composée de deux fonctions

Applications

Dans chacun des cas suivants, étudier la continuité de la fonction $f$ sur les intervalles de $D_f$ :

$$\begin{gathered} \overline{)1} f\left(x\right)=\sin \left(\frac{2x+1}{x^2-1}\right) \\ \overline{)2} f\left(x\right)=\sqrt{\frac{x-3}{x+2}} \\ \overline{)3} f\left(x\right)=\cos \left(\sqrt{x^2+1}\right) \\ \overline{)4} f\left(x\right)=\sqrt{1-\sin x} \\ \overline{)5} f\left(x\right)=\cos \left({\tan }^{2}x\right) \end{gathered}$$

III- Continuité d'une fonction numérique

3-7/ Composée d'une fonction continue et d'une fonction admettant une limite

Proposition 7

Soit $f$ une fonction définie sur l’ensemble $]x_0-r,x_0+r[ (r>0)$ et $g$ la fonction définie sur un intervalle ouvert $J$ centré en $\mathcal{l}$ tel que $f\left(I\right)\subset J$.

Si $\underset{x\to x_0}{\lim }f\left(x\right)=\mathcal{l}$ et $g$ est continue en $\mathcal{l}$ alors : $\underset{x\to x_0}{\lim }g\circ f\left(x\right)=g\left(\mathcal{l}\right)$

Remarque

La proposition 7 reste valable en $x_0$ à droite ou $x_0$ à gauche ou en $+\infty$ ou en $-\infty$ à condition de remplacer l’intervalle $I$ par un intervalle convenable.

III- Continuité d'une fonction numérique

3-7/ Composée d'une fonction continue et d'une fonction admettant une limite

Applications

Calculer les limites suivantes :

$$\begin{gathered} \overline{)1} \underset{x\to +\infty }{\lim }{\left(x-2\sqrt{x}+\frac{1}{x}\right)}^3 \\ \overline{)2} \underset{x\to 0}{\lim }\tan \left(\frac{\mathrm{\pi sinx}}{3x}\right) \\ \overline{)3} \underset{x\to -\infty }{\lim }\cos \left(\frac{\mathrm{\pi x}+1}{x+2}\right) \\ \overline{)4} \underset{x\to +\infty }{\lim }\cos \left(\sin \left(\frac{1}{x}\right)\right) \end{gathered}$$

IV- Image d'un intervalle par une fonction continue

4-1/ Image d'un segment par une fonction continue

Proposition 8

L'image d'un segment par une fonction continue est un segment.

Autrement dit :

($f$ continue sur $[a,b])\Rightarrow f([a,b])=[m, M ]$

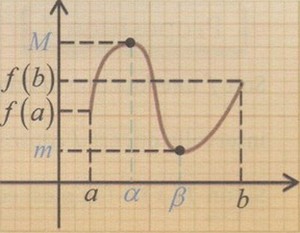
Remarque

Si $f$ est continue sur un segment $[a,b]$, alors $M=f\left(\alpha \right)$ est le ntaximum de $f$ sur $[a,b]$ et $m=f\left(\beta \right)$ est le minimum de $f$ sur $[a,b]$.

On a alors : $f\left([a,b]\right)=[m, M ]$

IV- Image d'un intervalle par une fonction continue

4-1/ Image d'un segment par une fonction continue

Proposition 9

L'image d'un intervalle par une fonction continue est un intervalle.

Remarque

La continuité d'une fonction est une condition suffisante pour que l'image d'un intervalle soit un intervalle, mais cette condition n'est pas évidemment nécessaire.

En effet, il se peut que l'image d'un intervalle par une fonction discontinue soit un intervalle comme le montre l'exemple suivant :

Considérons la fonction $f$ définie sur $\left[-1;2\right]$ par :

$\left\{\begin{array}{l}f\left(x\right)=2x si x\in \left[-1;1\right]\\ f\left(x\right)=x-1 si x\in ]1;2]\end{array}\right.$

L'image de l'intervalle $\left[-1;2\right]$ par la fonction $f$ est l'intervalle $[-2;2]$ bien que la fonction $f$ ne soit pas continue sur $\left[-1;2\right]$.

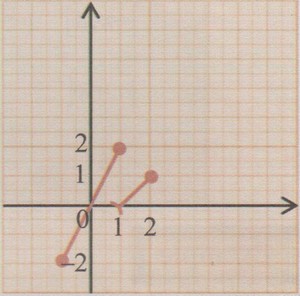
Les intervalles $I$ et $f\left(I\right)$ ne sont pas toujours de même nature. A titre d'exemple, l'image de l'intervalle semi-ouvert $]—1;2]$ par la fonction $x\mapsto x^2$ est le segment $[0;4]$.

IV- Image d'un intervalle par une fonction continue

4-1/ Image d'un segment par une fonction continue

Applications

Pour chacun des cas suivants, montrer que la fonction $f$ est continue sur l’intervalle $I$, puis déterminer $f\left(I\right)$ :

$$\begin{gathered} \overline{)1} f\left(x\right)=x^2+2 ; I=\left[-1;3\right] \\ \overline{)2} f\left(x\right)=\frac{x-4}{x-2} ; I=\left[5;8\right] \\ \overline{)3} f\left(x\right)=2x\sqrt{x+1} ; I=\left[3;5\right] \\ \overline{)4} \left\{\begin{array}{l}f\left(x\right)=x+3 si x\le 2\\ f\left(x\right)=x^2+1 si x>2\end{array}\right. ; I=\left[-3;5\right] \end{gathered}$$

IV- Image d'un intervalle par une fonction continue

4-2/ Image d'un intervalle par une fonction continue et strictement monotone

Soit $f$ une fonction continue et strictement monotone sur un intervalle $I$.

On a alors les résultats suivants :

IV- Image d'un intervalle par une fonction continue

4-2/ Image d'un intervalle par une fonction continue et strictement monotone

Soit $f$ la fonction numérique définie sur $\mathrm{ℝ}$ par : $f\left(x\right)=x^2-2x+3$

Déterminer les images des intervalles suivants par la fonction $f$ :

$I=]-\infty ;0] - J=\left[1;2\right] - K=]-5;-1[ - L=[\sqrt{2};+\infty [$

IV- Image d'un intervalle par une fonction continue

4-3/ Théorème des valeurs intermédiaires

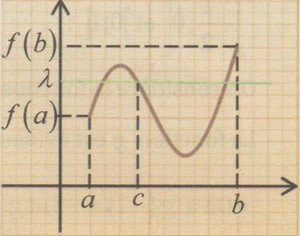
Proposition 10

Si $f$ une fonction continue sur un intervalle $[a,b]$ alors, pour tout réel $\lambda$ compris entre $f\left(a\right)$ et $f\left(b\right)$ il existe au moins un réel $c$ appartenant à l'intervalle $[a,b]$ tel que $f\left(c\right)=\lambda$.

En d'autres termes : l'équation $f\left(x\right)=\lambda$ d'inconnue $x$ admet au moins une solution dans $[a,b]$, pour tout $\lambda$ compris entre $f\left(a\right)$ et $f\left(b\right)$.

Corollaire

Si la fonction $f$ est continue sur $[a,b]$ tel que $f\left(a\right).f\left(b\right)<0$ alors l'équation $f\left(x\right)=0$ admet au
moins une solution dans l'intervalle $[a,b]$.

Si de plus, la fonction $f$ est strictement monotone, cette solution est unique.

Remarque

On peut interpréter le résultat du corollaire précédent comme suit :

Si la fonction $f$ est continue sur $[a,b]$ et si $f\left(a\right)$ et $f\left(b\right)$ sont de signes contraires, alors le graphe coupe l'axe des abscisses, au moins une fois, en un point dont l'abscisse appartient à $[a,b]$.

IV- Image d'un intervalle par une fonction continue

4-3/ Théorème des valeurs intermédiaires

Applications

1. Montrer que chacune des équations suivantes admet au moins une solution dans l'intervalle $I$ :

$$\begin{gathered} \overline{)1} x^4+x^2+4x-1=0 ; I=\left[0;1\right] \\ \overline{)2} 2\cos x-x=0 ; I=\left[0;\mathrm{\pi }\right] \\ \overline{)3} 1+\sin x=4x ; I=\left[0;\frac{\mathrm{\pi }}{2}\right] \\ \overline{)4} \tan x+x^2=2 ; I=]\frac{\mathrm{\pi }}{4};\frac{\mathrm{\pi }}{3}[ \end{gathered}$$

2. Montrer que l'équation $x^3-6x^2+6=0$ admet une solution unique dans l’intervalle $[-2;0]$.

Soit $f$ une fonction continue sur un intervalle $I$ de $\mathrm{ℝ}$ telle que : $\left(\forall x\in I\right) f\left(x\right)\ne 0$

3. Montrer par l'absurde que la fonction $f$ garde un signe constant sur l’intervalle $I$.

IV- Image d'un intervalle par une fonction continue

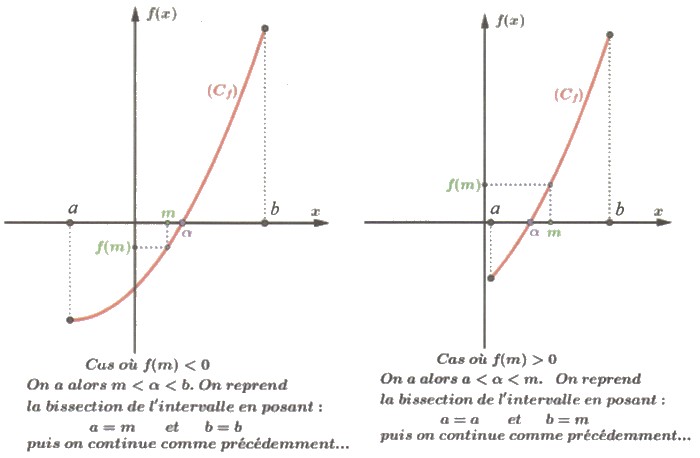
4-4/ Principe de la méthode de dichotomie

Soit $f$ une fonction continue sur un segment $[a,b]$ telle que l'équation $f\left(x\right)=0$ admet une solution unique $\alpha$ dans $[a,b]$.

Pour déterminer un encadrement du nombre $\alpha$, on démarre donc en ayant localisé la racine $\alpha$ entre $a$ et $b$ $(a<\alpha <b)$ ; et on sait par exemple que sur cet intervalle, la fonction $f$ (continue) est strictement croissante.

On calcule alors le centre $m$ du segment $[a,b]$ (à savoir $m=\frac{a+b}{2}$), puis son image par $f$ : $f\left(m\right)$, et on la compare à $0$.

Deux cas peuvent alors se produire :