
Physique et Chimie : 2ème Année Bac
Séance 26A (Aspects énergétiques des oscillateurs mécaniques – Pendule élastique)
Professeur : Mr EL GOUFIFA Jihad
Sommaire
I- Travail de la tension d’un ressort
1-1/ Travail d’une force constante
1-2/ Travail de la tension d'un ressort
II- Étude énergétique du pendule élastique
2-1/ L’énergie cinétique
2-2/ L’énergie potentielle
2-3/ Conservation de l'énergie mécanique
2-4/ Détermination de l'équation différentielle par étude énergétique
III- Diagrammes énergétiques
3-1/ Cas des oscillations sans frottements
3-2/ Cas des oscillations avec frottements
IV- Exercices
4-1/ Exercice 1
4-2/ Exercice 2
4-3/ Exercice 3
I- Travail de la tension d’un ressort
1-1/ Travail d’une force constante
Le travail d'une force constante entre deux points A et B est égale au produit scalaire du vecteur force par le vecteur déplacement :
avec en joule (J), en newton (N), en mètre (m) et

I- Travail de la tension d’un ressort
1-2/ Travail de la tension d'un ressort
Considérons un ressort de longueur initiale et de constante de raideur placé sur un plan horizontal :

La tension du ressort. n'est pas une force constante.
Pour calculer le travail de cette force on doit considérer le travail élémentaire de cette force sir un déplacement infiniment petit sur lequel nous considérerons que la force est constante :
Le travail total de la tension du ressort lorsque son point d'application se déplace d'un point d'abscisse à un point d'abscisse est la somme des travaux élémentaires, on l'obtient en utilisant le calcul intégral :
II- Étude énergétique du pendule élastique
2-1/ L’énergie cinétique
C’est l’énergie qu’un corps possède du fait de son mouvement, son unité est Joules (J).
Elle est donné par la relation suivante :
II- Étude énergétique du pendule élastique
2-2/ L’énergie potentielle
L'énergie potentielle élastique d'un pendule élastique est l'énergie qu'il possède grâce à la déformation du ressort.
Elle est égale au travail que doit effectuer un opérateur pour le déformer.
Elle est donnée par la relation suivante :
II- Étude énergétique du pendule élastique
2-3/ Conservation de l'énergie mécanique
Pendant les oscillations libres non amorties d'un pendule élastique horizontal constitué d'un corps S de masse m et d'un ressort de constante de raideur K, appliquons le théorème de l'énergie cinétique sur le corps S entre un point d'abscisse et un point d'abscisse :
On a :
Donc lorsque les frottements sont absents, l’énergie mécanique se conserve.
II- Étude énergétique du pendule élastique
2-4/ Détermination de l'équation différentielle par étude énergétique
Si les frottement sont négligeables, l'énergie mécanique de l'oscillateur est constante :
C’est la même équation différentielle obtenue à partir l’étude dynamique.
III- Diagrammes énergétiques
3-1/ Cas des oscillations sans frottements
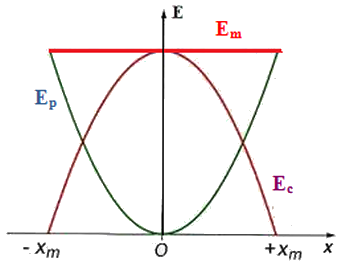
Dans le cas des oscillations sans frottements l'énergie mécanique de l'oscillateur mécanique est constante :
En représentant la variation , et en fonction de on obtient le diagramme suivant :
En représentant la variation , et en fonction du temps on obtient le diagramme suivant :

III- Diagrammes énergétiques
3-2/ Cas des oscillations avec frottements
Dans le cas des oscillations avec frottements l'énergie mécanique de l'oscillateur mécanique diminue jusqu'à ce qu'elle s'annule :

IV- Exercices
4-1/ Exercice 1
On relie un corps solide , de masse , à un ressort à spires non jointive, de masse négligeable et de raideur , et on fixe l’autre bout du ressort à un support fixe :
Le corps peut glisser sans frottement sur un plan horizontal.
On écarte le corps de sa position d’équilibre de la distance , et on le libère sans vitesse initiale.
Pour étudier le mouvement de , on choisie le référentiel galiléen tel que la position de à l’origine des dates est confondue avec l’origine .
On repère la position de à l’instant par l’abscisse dans le repère .
L’équation différentielle du mouvement de s’écrit , et sa solution est de la forme .
L’étude expérimentale du mouvement de a permis d’obtenir le graphe représenté sur la figure suivante :
- Déterminer en exploitant le graphe les grandeurs suivantes : l’amplitude , la période et la phase à l’origine des dates.
- En déduire la raideur du ressort.
On choisi le plan horizontal passant par la position de à l’équilibre comme origine de l’énergie potentielle de pesanteur et l’état où le ressort n’est pas déformé comme origine de l’énergie potentielle élastique.
- Montrer que l’énergie cinétique du corps s’écrit :
- Trouver l’expression de l’énergie mécanique du système {corps - ressort} en fonction de et et en déduire la vitesse lorsque passe par la position d’équilibre dans le sens positif.
IV- Exercices
4-2/ Exercice 2
Les ressorts se trouvent dans plusieurs appareils mécaniques, comme les voitures et les bicyclettes... et produisent des oscillations mécaniques.
Cette exercice a pour objectif l’étude énergétique d’un système oscillant {corps solide - ressort} dans une position horizontale.
Soit un oscillateur mécanique horizontal composé d’un corps solide de masse m et de centre d’inertie fixé à l’extrémité d’un ressort à spires non jointives et de masse négligeable et de raideur .
L’autre extrémité du ressort est fixée à un support fixe.
Le corps glisse sans frottement sur le plan horizontal.
On étudie le mouvement de l’oscillateur dans le repère lié à la Terre et dont l’origine est confondue avec la position de G à l’équilibre de .
On repère la position de à l’instant par son abscisse :
On écarte le corps horizontalement de sa position d’équilibre dans le sens positif d’une distance et on le libère sans vitesse initiale à l’instant pris comme origine des dates.
On choisie le plan horizontal passant par comme référence de l’énergie potentielle de pesanteur, et l’état dans lequel le ressort n’est pas déformé comme référence de l’énergie potentielle élastique.
À l’aide d’un dispositif informatique adéquat, on obtient les deux courbes représentant les variations de l’énergie cinétique et l’énergie potentielle élastique du système oscillant en fonction du temps :
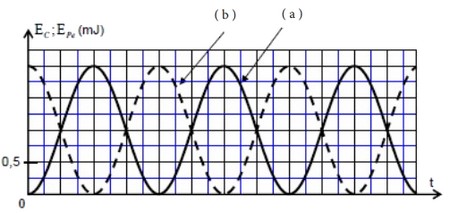
- Indiquer parmi les courbes (a) et (b) celle qui représente les variations de l’énergie cinétique . Justifier votre réponse.
- Déterminer la valeur de l’énergie mécanique du système oscillant.
- En déduire la valeur de la distance .
- En considérant la variation de l’énergie potentielle élastique du système oscillant, trouver le travail de la force de rappel exercée par le ressort sur lors du déplacement de de la position d’abscisse vers la position .
IV- Exercices
4-3/ Exercice 3
Un oscillateur mécanique vertical est constitué d’un corps solide de masse et d’un ressort à spires non jointives de masse négligeable et de raideur .
L’une des extrémités du ressort est fixée à un support fixe et l’autre extrémité est liée au solide :

On se propose d’étudier le mouvement du centre d’inertie du solide dans un repère lié à un référentiel terrestre supposé galiléen.
On repère la position de à un instant par la côte sur l’axe .
À l’équilibre, est confondu avec l’origine du repère .
On prendra .
Frottements négligeables
On écarte verticalement le solide de sa position d’équilibre et on l’envoie à l’instant de date , avec une vitesse initiale .
La courbe suivante représente l’évolution de la côte du centre d’inertie :

- Déterminer, à l’équilibre, l’allongement du ressort en fonction de , et de l’intensité de la pesanteur .
- Établir l’équation différentielle vérifiée par la côte du centre d’inertie .
La solution de cette équation différentielle s’écrit , avec la période propre de l’oscillateur.
- Déterminer la valeur de et celle de .
Frottements non négligeables
On réalise deux expériences en plongeant l’oscillateur dans deux liquides différents.
Dans chaque expérience, on écarte verticalement le solide de sa position d’équilibre d’une
distance et on l’abandonne sans vitesse initiale à l’instant , le solide oscille alors à l’intérieur du liquide.
Les courbes (1) et (2) de la figure suivante représentent l’évolution de la côte z du centre d’inertie G au cours du temps dans chaque liquide :

- Associer à chaque courbe le régime d’amortissement correspondant.
On choisit le plan horizontal auquel appartient le point , origine du repère , comme état de référence de l’énergie potentielle de pesanteur , et l’état où le ressort est non déformé comme état de référence de l’énergie potentielle élastique .
- Pour les oscillations correspondant à la courbe (1), trouver à un instant de date , l’expression de l’énergie potentielle en fonction de , et l’allongement du ressort à l’équilibre dans le liquide.
- Pour les oscillations correspondant à la courbe (1), calculer la variation de l’énergie mécanique de l’oscillateur entre les instants et .


