
Physique et Chimie : 2ème Année Bac
Séance 24A (Oscillateurs mécaniques – Pendule élastique)
Professeur : Mr EL GOUFIFA Jihad
Sommaire
I- Systèmes mécaniques oscillants
1-1/ Définition
1-2/ Exemples de quelques oscillateurs mécaniques
1-3/ Caractéristiques des mouvements oscillatoires
1-4/ Amortissement des oscillations
II- Pendule élastique horizontal
2-1/ Équation différentielle du mouvement
2-2/ Équation horaire du mouvement
III- Pendule élastique vertical
IV- Pendule élastique incliné
V- L’amortissement des oscillations
VI- Exercices
6-1/ Exercice 1
6-2/ Exercice 2
6-3/ Exercice 3
I- Systèmes mécaniques oscillants
1-1/ Définition
Un système oscillant, est tout simplement un corps ou plusieurs corps, effectuent un mouvement d’aller-retour autour de son position d’équilibre.
Lors de cette étude, on remarquera une analogie entre les systèmes oscillants (le pendule élastique, de torsion, pesant...) et les circuits (LC, RLC...). On parle des oscillateurs harmoniques.
I- Systèmes mécaniques oscillants
1-2/ Exemples de quelques oscillateurs mécaniques
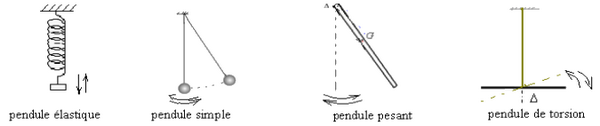
- Le pendule élastique : il est constitué d'un corps solide de masse m suspendu à un ressort à spires non jointives.
- Le pendule simple : il est constitué d'un corps solide de masse m suspendu à l’extrémité d'un fil inextensible.
- Le pendule pesant : est tout corps solide mobile autour d'un axe ne passant pas par son centre de gravité
- Le pendule de torsion : est constitué d'une barre horizontale, fixée à l’extrémité d'un fil de torsion.
I- Systèmes mécaniques oscillants
1-3/ Caractéristiques des mouvements oscillatoires
Un mouvement oscillatoire est caractérisé par :
- Sa position d'équilibre stable : C'est la position à laquelle le système tend à y revenir lorsque l'on en éloigne légèrement.
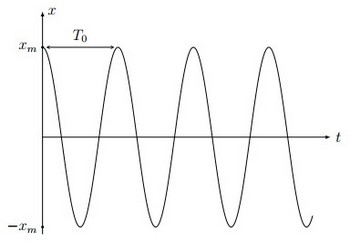
- Sa période propre : C'est le temps mis pour effectuer une oscillation.
- Son amplitude : C'est la valeur maximale positive que prend la grandeur qui exprime le décalage ou l'inclinaison de l'oscillateur de sa position d'équilibre.
I- Systèmes mécaniques oscillants
1-4/ Amortissement des oscillations
Définition
En écartant un pendule élastique de sa position d'équilibre et en le lâchant, l'amplitude des oscillations diminue jusqu'à ce qu'il s'annule: on dit que le mouvement est amorti. Le phénomène d'amortissement est provoqué par les frottements.
Il existe deux types de frottements :
- Le frottement solide qui se fait entre l'oscillateur et un corps solide.
- Le frottement fluide qui se fait entre l'oscillateur et un corps fluide (liquide ou gaz).
I- Systèmes mécaniques oscillants
1-4/ Amortissement des oscillations
Les régimes d'amortissement
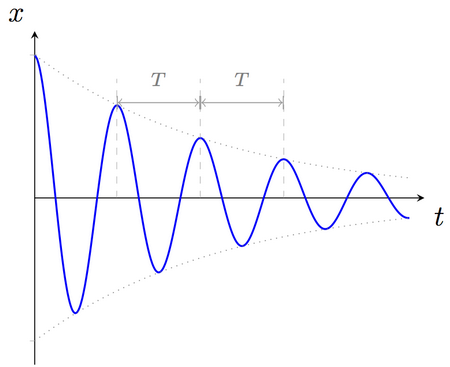
Le régime pseudo périodique :
Si l'amortissement est faible, l'amplitude des oscillations diminue progressivement jusqu'à ce qu'il s'annule.
Le régime apériodique :
Si le frottement est fort les oscillations disparaissent et selon l'importance de l'amortissement on distingue trois régimes :
- Le régime sous critique : l'oscillateur effectue une seule oscillation avant de s'arrêter.
- Le régime critique : l'oscillateur revient à sa position d'équilibre sans oscillations.
- Le régime surcritique : l'oscillateur revient à sa position d'équilibre après temps très long sans oscillations.

II- Pendule élastique horizontal
2-1/ Équation différentielle du mouvement
Sur un plan lisse on attache à l’extrémité d’un ressort de spires non jointives et de masse négligeable, un corps (S) de masse m, on l’écarte de sa position d’équilibre, et on le lâche sans vitesse initiale, le solide effectue donc un mouvement rectiligne.oscillatoire.
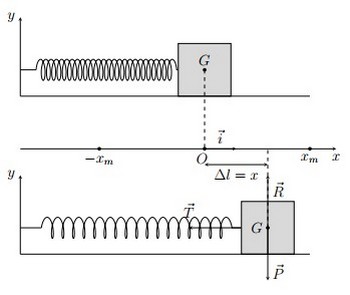
Bilan des forces :
- : Le poids du corps
- : La réaction du plan
- : La tension du ressort
On applique la deuxième loi de Newton :
C'est l'équation différentielle du mouvement
II- Pendule élastique horizontal
2-2/ Équation horaire du mouvement
La solution de l'équation différentielle du mouvement est une fonction sinusoïdale qui s'écrit sous la forme :
- : Abscisse (élongation) du point G et varie entre et
- : Amplitude ou élongation maximale
- : pulsation (rad/s)
- : la période propre (s)
- : Phase à l’instant t
- : Phase à l’origine des temps t=0
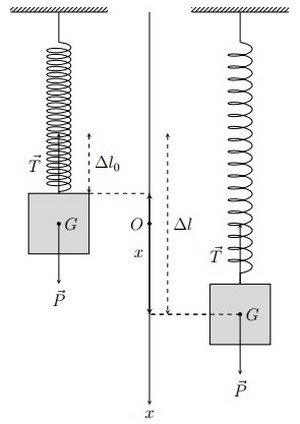
II- Pendule élastique vertical
À l’extrémité libre d’un ressort de spires non jointives et de masse négligeable, on attache un corps (S) de masse m.
Dans ce cas il faut faire attention en ce qui concerne l’élongation du ressort, car lors du suspension du corps, le ressort s’allonge d’une distance .
Pour la déterminer on étudie le système en équilibre :
|
Bilan des forces :
On applique la première loi de Newton : |
 |
III- Pendule élastique vertical
En allongeant le corps (S) vers le bas, il effectue un mouvement oscillatoire, on suppose que l’air n’a aucun effet sur le mouvement de (S) :
|
Bilan des forces :
On applique la deuxième loi de Newton : |
 |
C’est la même équation différentielle obtenue dans la section précédente, sa solution est toujours de la forme :
IV- Pendule élastique incliné
Dans un plan lisse incliné d’un angle α, on attache à l’extrémité d’un ressort de spires non jointives et de masse négligeables, un corps (S) de masse m, le ressort s’allonge donc d’une distance , on la détermine en étudiant le système à l’équilibre :

Bilan des forces :
- : Le poids du corps
- : La tension du ressort
- : La réaction du plan
On applique la première loi de Newton :
IV- Pendule élastique incliné
Maintenant on écarte le corps, et on le lâche sans vitesse initiale, il effectue un mouvement oscillatoire :
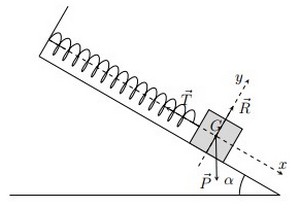
Bilan des forces :
- : Le poids du corps
- : La tension du ressort
- : La réaction du plan
On applique la deuxième loi de Newton :
C’est la même équation différentielle obtenue dans la section précédente, sa solution est toujours de la forme :
V- L’amortissement des oscillations
En réalité, les frottements ne sont pas négligeables, ceci constitue un obstacle devant le mouvement oscillatoire du corps.
Le corps n’atteint plus , sa vitesse et son accélération décroient, et sur l’enregistrement on observe :

VI- Exercices
6-1/ Exercice 1
Un oscillateur mécanique élastique est constitué d’un ressort de constante de raideur associé à un solide de masse .
On écarte le système de sa position d’équilibre de et on l’abandonne sans vitesse initiale.
On considère un axe , avec coïncide avec la position du centre d’inertie du solide à l’équilibre et le vecteur unitaire parallèle au déplacement du solide.
On repère la position du solide à chaque instant par l’élongation :

- Montrer que le mouvement du centre d’inertie du solide obéit, en absence de frottement, à l’équation différentielle suivante : .
La solution de cette équation différentielle est de la forme .
- Déterminer l’expression de la période propre des oscillations du pendule élastique et calculer sa valeur.
- Déterminer les paramètres et , sachant qu’à l’instant , passe par la position d’équilibre du pendule dans le sens positif, écrire cette solution.
- Déterminer la vitesse des oscillation à l’instant , en déduire la vitesse maximale du système en précisant sa positions.
- Déterminer les caractéristiques de la force exercée par le ressort sur le solide dans les deux cas suivant :
- lorsque le solide passe par sa position d’équilibre stable.
- lorsque et .
VI- Exercices
6-2/ Exercice 2
Un pendule élastique vertical est constitué d’un ressort de constante de raideur associé à un solide de masse .
On écarte le système de sa position d’équilibre de , et à l’instant (origine des dates) on l’abandonne avec une vitesse initiale dans le sens négatif de l’axe orienté vers le bas, et avec coïncide avec la position du centre d’inertie du solide à l’équilibre stable et le vecteur unitaire parallèle au déplacement du solide.
On repère la position du solide à chaque instant par l’élongation :

- Montrer que le mouvement du centre d’inertie du solide obéit, en absence de frottement, à l’équation différentielle suivante :
La solution de cette équation différentielle est de la forme : .
- Déterminer l’expression de la période propre des oscillations du pendule élastique et calculer sa valeur.
- Déterminer les paramètres et .
Étudions le cas où on lance le système à , à partir de l’état d’équilibre stable, dans le sens positive avec une vitesse .
- Déterminer les paramètres et .
VI- Exercices
6-3/ Exercice 3
On place un cavalier de masse sur un rail à coussin d’air horizontal et on le fixe aux extrémités de deux ressorts semblables et de mêmes constantes de raideur .
La longueur initiale de chaque ressort est , et à l’équilibre, ils ont même allongement :
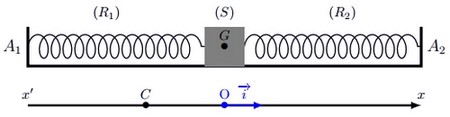
On écarte le cavalier de sa position d’équilibre de distance de sens vers et de direction de , puis on l’abandonne sans vitesse initiale, à l’instant .
- Déterminer, à un instant , les expressions des allongements de et pour chaque ressort en fonction de l’abscisse de .
- Déterminer l’équation différentielle du mouvement de .
La solution de cette équation différentielle s’écrit sous la forme suivante , avec est la pulsation propre du mouvement de .
- Donner l’expression de et .
- Déterminer et .
On fixe au cavalier une petite plaque de masse négligeable puis on l’immerge dans un liquide.
La force de frottement appliquée par le liquide sur la plaque au cours du mouvement du cavalier est de la forme , où est une constante positive et le vecteur vitesse de .
- Montrer que l’équation différentielle du mouvement de peut s’écrire sous la forme suivante :
- Donner la forme des courbes qui représentent l’élongation du centre d’inertie lorsque les frottement deviennent de plus en plus importants. (on prend les mêmes conditions initiales)


