
Physique et Chimie : 2ème Année Bac
Séance 23 (Mouvement de rotation d’un solide autour d’un axe fixe)
Professeur : Mr El GOUFIFA Jihad
Sommaire
I- Introduction
II- Abscisse angulaire, vitesse angulaire et accélération angulaire
2-1/ Définition
2-2/ Abscisse angulaire et abscisse curviligne
2-3/ Vitesse angulaire et vitesse linéaire
2-4/ Accélération angulaire et accélération linéaire
III- Mouvement de rotation
3-1/ Mouvement de rotation uniforme
3-2/ Mouvement de rotation uniformément varié
IV- Le Principe Fondamentale de la Dynamique (PFD)
4-1/ Énonce du principe fondamentale de la dynamique
4-2/ Comment exploiter la relation fondamentale de la dynamique
4-3/ Moment d'une force par rapport à un axe fixe
4-4/ Expression du moment d'inertie de quelques corps solides
V- Exercices
5-1/ Exercice 1
5-2/ Exercice 2
5-3/ Exercice 3
I- Introduction
Sous l’action d’un ensemble de forces, la grande roue est animée d’un mouvement de rotation autour d’un axe fixe.
Un tel mouvement est caractérisé, à chaque instant, par son accélération angulaire.
- Qu’est ce que l’accélération angulaire ?
- Quelle relation la relie aux moments des forces appliquées à la grande roue ?

II- Abscisse angulaire, vitesse angulaire et accélération angulaire
2-1/ Définition
Un mouvement de rotation est tout mouvement qu’effectue un corps autours d’un axe fixe selon une trajectoire circulaire de rayon autour de cet axe.
II- Abscisse angulaire, vitesse angulaire et accélération angulaire
2-2/ Abscisse angulaire et abscisse curviligne
On peut déterminer la position d’un point en mouvement le long d’un trajet circulaire de rayon soit par :
- Les coordonnées cartésiennes dans un référentiel :
- L’abscisse angulaire tel que
- L’abscisse curvilignes , et c’est l’arc avec .
II- Abscisse angulaire, vitesse angulaire et accélération angulaire
2-3/ Vitesse angulaire et vitesse linéaire
On définit la vitesse angulaire comme la dérivée de l’abscisse angulaire par rapport au temps :
Son unité .
La relation entre la vitesse angulaire et la vitesse linéaire est :

II- Abscisse angulaire, vitesse angulaire et accélération angulaire
2-4/ Accélération angulaire et accélération linéaire
On définit l’accélération angulaire comme la dérivée de la vitesse par rapport au temps :
Son unité est .
D’après la relation de Frenet on a :
On a :

III- Mouvement de rotation
3-1/ Mouvement de rotation uniforme
Le mouvement de rotation uniforme est un mouvement dans lequel l’accélération angulaire est nulle, et la vitesse est constante.
Son équation horaire est :
est l’abscisse angulaire à l’origine des dates.
III- Mouvement de rotation
3-2/ Mouvement de rotation uniformément varié
Le mouvement de rotation varié est un mouvement dans lequel l’accélération est constante, son équation horaire est :
est la vitesse angulaire à l’origine des dates.
L’équation de la vitesse angulaire est :
De cette équation on peut déduire que
En remplaçant dans l’équation horaire :
C’est la relation caractéristique du mouvement de rotation uniformément varié.
IV- Le Principe Fondamentale de la Dynamique (PFD)
4-1/ Énonce du principe fondamentale de la dynamique
La somme des moments des forces extérieures qui s’exercent sur un solide en rotation autour d’un axe fixe est égale au moment d’inertie du solide multiplié par son accélération angulaire.
- : Moment d'inertie du corps solide en
- : Accélération angulaire en
Si , le solide est en mouvement de rotation uniforme.
Si , le solide est en mouvement de rotation uniformément varié.
IV- Le Principe Fondamentale de la Dynamique (PFD)
4-2/ Comment exploiter la relation fondamentale de la dynamique
Pour résoudre un problème de dynamique en utilisant la PFD, la méthode est toujours la même :
- Préciser le système à étudier.
- Faire le bilan de toutes les forces qui agissent sur le point matériel étudié (ou le centre d’inertie de l’objet étudié).
- Faire un schéma précis et suffisamment grand pour pouvoir y représenter (tant que c’est possible) toutes les forces dont les caractéristiques bien connues.
- Choisir un sens positif de rotation (Souvent identique au sens de mouvement).
- Déterminer l’expression du moment de chacune des forces du bilan.
- Appliquer la PFD.
- Répondre.
IV- Le Principe Fondamentale de la Dynamique (PFD)
4-3/ Moment d'une force par rapport à un axe fixe
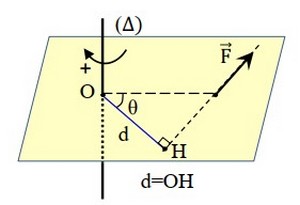
Le moment d’une force par rapport à un axe fixe , est le produit de l’intensité de cette force par la distance qui sépare la droite d’action de la force et l’axe de rotation.
Le signe dépend du sens de rotation, si la force tourne le solide dans le sens positif alors le signe est positif, sinon le signe du est négatif.
Son unité est .
Physiquement, c’est la grandeur qui traduit l’aptitude de cette force de faire tourner un système mécanique autour d’un axe.
IV- Le Principe Fondamentale de la Dynamique (PFD)
4-4/ Expression du moment d'inertie de quelques corps solides
Le moment d’inertie d’un corps est l’analogue de la masse , c’est une quantité physique caractérisant chaque corps, elle dépend de la masse, la longueur, la forme...
Son unité est
Le moment d’inertie d’un corps varie si :
- On ajoute des masses au système.
- On modifie la position d’au corps du système.
- La position de l’axe change.
Exemples

V- Exercices
5-1/ Exercice 1
On considère un corps de masse capable de glisser sans frottement sur un plan incliné d'un angle par rapport à la ligne horizontale.
Le corps est fixé par extrémité inférieure à un fil inextensible de masse négligeable et enroulé sur un cylindre homogène de rayon capable de tourner sans frottement autour d'un axe horizontal et fixe .
On donne : et .
On libère le corps du point sans vitesse initiale et il glisse sans frottement sur le plan incliné provoquant la rotation du cylindre.
- Déterminer l'accélération du corps et en déduire la nature de son mouvement.
- Déterminer la vitesse du corps au point sachant que .
Au point le fil se détache du cylindre à un instant et le corps tombe au point d'une altitude .
- Donner les équations horaires du mouvement du centre d'inertie du corps dans le repère .
- En déduire la durée de chute du corps et la distance .
Lorsque le fil se détache du cylindre, ce dernier est soumis à un couple résistant de moment constant , et il s'arrête de tourner après avoir effectué plusieurs tours.
- Déterminer l'accélération angulaire du cylindre.
- Quel est le nombre de tours effectué par le cylindre durant le freinage.
V- Exercices
5-2/ Exercice 2
On considère une poulie à double gorge de rayons et qui peut tourner sans frottement autour d'un axe fixe.
Les deux corps et sont suspendus par deux fils inextensibles enroulés sur les poulies comme l'indique la figure :
Moment d'inertie de la poulie à double gorge :
- Déterminer l'expression de en fonction de , et pour que la poulie reste en équilibre.
On utilise par la suite et et on libère le système sans vitesse initiale à un instant .
- Déterminer le sens du mouvement.
- Montrer que l'accélération angulaire du système des deux poulies est :
- Calculer sa valeur.
- Quel est le nombre de tours effectués par le système des deux poulies pendant la durée ?
V- Exercices
5-3/ Exercice 3
Une poulie de rayon et de moment d'inertie est mobile autour de l'axe horizontal passant par son centre.
On enroule sur la gorge de cette poulie un fil inextensible de masse négligeable.
A l'extrémité libre du fil, on accroche un solide de masse . Le solide supposé ponctuel se trouve à une hauteur au-dessus du sol.
On abandonne le système à lui-même sans vitesse initiale à l'instant .
- Montrer que le mouvement de est rectiligne uniformément varié. Calculer son accélération.
Une seconde après le début du mouvement, le fil supportant le solide se détache de la poulie.
- Avec quelle vitesse et au bout de combien de temps le solide atteint-il le sol ?
- Quelle est la nature du mouvement ultérieure de la poulie (après détachement du fil ?
- Écrire l'équation horaire de ce mouvement. On prendra comme origine des abscisses angulaires la position du rayon à l'instant de date .
On applique à la poulie un couple de freinage de moment constant. La poulie s'arrête après avoir effectué 10 tours en mouvement de rotation uniformément retardé.
- Calculer le moment du couple de freinage.


