Séance 22 - Mouvement des satellites et des planètes

Sommaire

I- Référentiel héliocentrique et géocentrique

II- L’ellipse

III- Les lois de Kepler

3-1/ Loi des orbites

3-2/ Loi des aires

3-3/ Loi des périodes

IV- Étude du mouvement d’une planète et d’un satellite

4-1/ Rappel sur la loi d’attraction universelle

4-2/ Étude du mouvement d’une planète autour du soleil

4-3/ Étude du mouvement d’un satellite en orbite

4-4/ Les satellites géostationnaires

V- L'impesanteur

VI- Exercices

6-1/ Exercice 1

6-2/ Exercice 2

6-3/ Exercice 3

I- Référentiel héliocentrique et géocentrique

Le repère héliocentrique

Un repère dont l’origine est confondue avec le centre d’inertie du système solaire, c’est-à-dire le centre du soleil, ses trois axes sont dirigés vers 3 étoiles fixes.

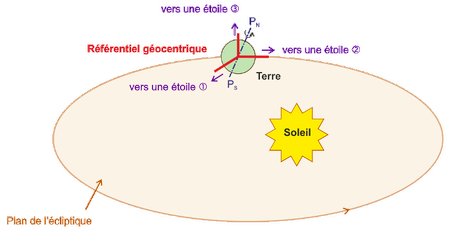
Le repère géocentrique

Un repère dont l’origine est confondue avec le centre d’inertie de la terre, ses trois axes dont deux sont dans le plan de l’équateur dirigés vers 2 étoiles fixes, et le troisième est dirigé vers l’étoile polaire.

II- L’ellipse

En géométrie, une ellipse est une courbe plane fermée obtenue par l’intersection d’un cône de révolution avec un plan, à condition que celui-ci coupe l'axe de rotation du cône ou du cylindre :

On peut également la définir comme le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante :

$PF+PF\text{'}=2a$

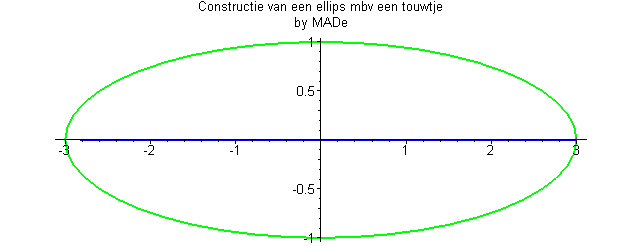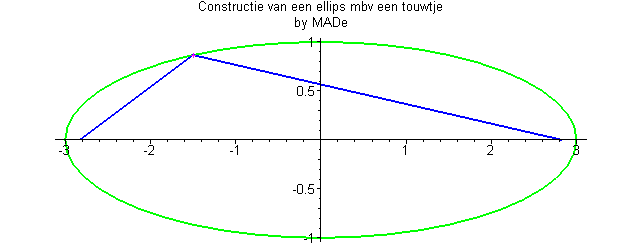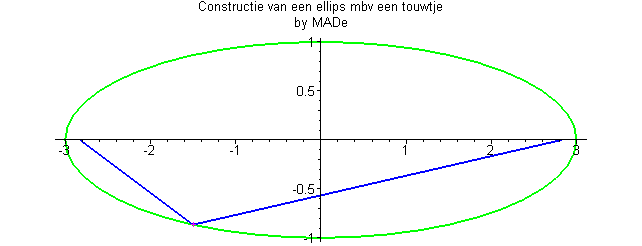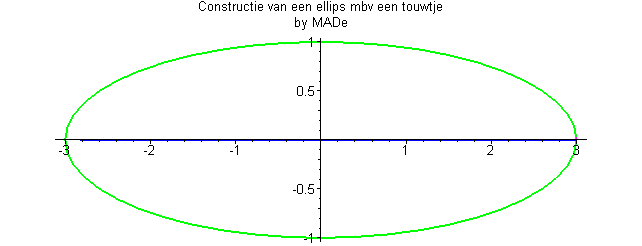
Le cercle est une ellipse dont les deux foyers sont confondus en un point appelé le centre, d’où : $a=r$ et $AA\prime =BB\prime =2r$

III- Les lois de Kepler

3-1/ Loi des orbites

Dans un référentiel héliocentrique, la trajectoire du centre d’une planète est une ellipse dont le centre du Soleil est l’un des foyers.

III- Les lois de Kepler

3-2/ Loi des aires

Le segment de la droite reliant le soleil à une planète balaie des aires égales pendant des durées égales.

Les planètes se déplacent plus rapidement lorsqu’elles sont proches du soleil et plus lentement lorsqu’elles sont plus éloignés.

$\overline{) {\mathcal{A}}_1={\mathcal{A}}_2 }$

III- Les lois de Kepler

3-3/ Loi des périodes

Pour toute planète du système solaire, le rapport entre le carré de la période de révolution et le cube du demi grand axe est constant :

$\overline{) \frac{T^2}{a^3}=Cte }$

Cette valeur dépend que du soleil, on remplace $r$ par $a$ lorsque la trajectoire est circulaire.

IV- Étude du mouvement d’une planète et d’un satellite

4-1/ Rappel sur la loi d’attraction universelle

La loi universelle de la gravitation ou loi de l'attraction universelle, découverte par Isaac Newton, est la loi décrivant la gravitation comme une force responsable de la chute des corps et du mouvement des corps célestes, et de façon générale, de l'attraction entre des corps ayant une masse, par exemple les planètes, les satellites naturels ou artificiels.

Lorsqu’il y a une interaction entre deux corps $A$ et $B$, le corps $A$ exerce une force sur le corps $B$, on la note ${\overrightarrow{F}}_{A/B}$, et le corps $B$ exerce une force de même intensité ${\overrightarrow{F}}_{B/A}$, ces deux vecteurs sont liés vectoriellement par la relation suivante :

$\overline{){\overrightarrow{ F}}_{A/B}=-{\overrightarrow{F}}_{B/A}=-G\frac{m_A{m}_B}{d^2}\overrightarrow{u}\overrightarrow{{}_{AB}} }$

$G$ est la constante de gravitation universelle elle vaut $6,67\times {10}^{-11}N.m^2.k{g}^{-2}$

$d=AB$ est la distance qui les sépare.

IV- Étude du mouvement d’une planète et d’un satellite

4-2/ Étude du mouvement d’une planète autour du soleil

La planète de masse $m$, est soumise qu’à la force d’attraction appliquée par le soleil :

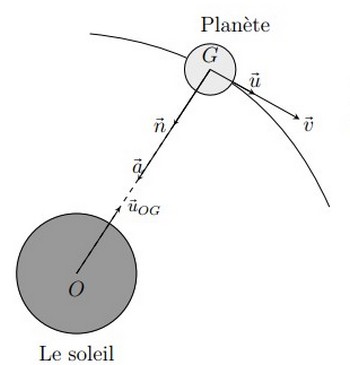
D’après la 2ème loi de Newton :

$$\begin{gathered} \sum _{}^{}\overrightarrow{F}=m\overrightarrow{a} \\ \Rightarrow G\frac{M_s.m}{r^2}\overrightarrow{n}=m\overrightarrow{a} \\ \Rightarrow \overline{)\overrightarrow{a}=\frac{G.M_s}{r^2}\overrightarrow{n}} \end{gathered}$$

Puisque le trajectoire est curviligne, alors d’après la relation de Frenet on aura :

$$\begin{gathered} \overrightarrow{a}=\frac{G.M_s}{r^2}\overrightarrow{n}=\frac{dv}{dt}\overrightarrow{u}+\frac{v^2}{r}\overrightarrow{n} \\ \Rightarrow \left\{\begin{array}{l}\frac{dv}{dt}=0\\ \frac{v^2}{r}=\frac{G.M_s}{r^2}\overrightarrow{n}\end{array}\right. \\ \Rightarrow \overline{)v=\sqrt{\frac{G.M_s}{r}}} \end{gathered}$$

Par suite le mouvement est circulaire uniforme, sa période est :

$$\begin{gathered} T=\frac{2\mathrm{\pi }}{\omega }=\frac{2\mathrm{\pi r}}{v}=\frac{2\mathrm{\pi r}}{\sqrt{\frac{G.M_s}{r}}} \\ {T}^2=\frac{4{\mathrm{\pi }}^2{\mathrm{r}}^2}{\frac{G.M_s}{r}}=\frac{4{\mathrm{\pi }}^2{\mathrm{r}}^3}{G.M_s} \\ \overline{)\frac{T^2}{{\mathrm{r}}^3}=\frac{4{\mathrm{\pi }}^2}{G.M_s}=Cte} \end{gathered}$$

D’où la constance du rapport $\frac{T^2}{{\mathrm{r}}^3}$ d’après la loi de Kepler.

IV- Étude du mouvement d’une planète et d’un satellite

4-3/ Étude du mouvement d’un satellite en orbite

Dans le référentiel géocentrique, étudions le mouvement, du centre d’inertie $G$ d’un satellite de la Terre, animé d’un mouvement circulaire de rayon $R$ (distance du satellite au centre de la Terre) :

Le système (le satellite de masse $m$) est soumis à la force gravitationnelle centripète $\overrightarrow{F}$ exercée par la Terre de masse $M_T$ :

Le référentiel géocentrique est galiléen, donc :

$$\begin{gathered} \sum _{}^{}\overrightarrow{F}=m\overrightarrow{a_G} \\ \Rightarrow G\frac{M_T.m}{R^2}\overrightarrow{n}=m\overrightarrow{a_G} \\ \Rightarrow \overline{)\overrightarrow{a_G}=\frac{G.M_T}{R^2}\overrightarrow{n}} \end{gathered}$$

Le vecteur accélération est centripète et sa valeur constante : le mouvement circulaire est donc uniforme de vitesse $v_G$ telle que :

$a_G=\frac{{v_G}^2}{R}=G.\frac{M_T}{R^2}$

Nous déduisons de cette égalité l’expression de la valeur de la vitesse :

$v_G=\sqrt{\frac{G.M_T}{R}}=\sqrt{\frac{G.M_T}{R_T+h}}$

où $R_T$ est le rayon terrestre et $h$ l’altitude du satellite.

La durée $T$ pour effectuer un tour, ou période de révolution, est égale à la longueur de la circonférence divisée par la valeur de la vitesse :

$T=\frac{2\pi R}{v_G}=2\pi \sqrt{\frac{{\mathrm{R}}^3}{G.M_T}} ; \left(R=R_T+h\right)$

En élevant cette expression au carré, on retrouve la troisième loi de KEPLER :

$\overline{)\frac{T^2}{{\mathrm{R}}^3}=\frac{4{\mathrm{\pi }}^2}{G.M_T}=Cte}$

IV- Étude du mouvement d’une planète et d’un satellite

4-4/ Les satellites géostationnaires

Considérons un satellite qui gravite, dans le référentiel géocentrique, sur une orbite circulaire, dans le plan de l’équateur terrestre et dans le même sens de rotation que la Terre autour de son axe :

Ce satellite est immobile par rapport à la Terre si sa période de révolution est égale à la période de rotation de la Terre autour de son axe.

Dans ce cas, il reste continuellement sur la verticale du même lieu de l’équateur (sur le rayon passant par ce lieu) : il est géostationnaire.

Calculons son altitude :

$$\begin{gathered} T=2\pi \sqrt{\frac{{\mathrm{R}}^3}{G.M_T}}=86 164s \\ {T}^2=\frac{4{\mathrm{\pi }}^2{\mathrm{R}}^3}{G.M_T} \\ R=\sqrt[3]{\frac{T^{2}G.M_T}{4{\mathrm{\pi }}^2}}=42 000Km \\ h=R-R_T\approx 36 000Km \end{gathered}$$

Conclusion

Dans le référentiel terrestre, les satellites géostationnaires évoluent sur une trajectoire circulaire, située dans le plan de l’équateur, à une altitude voisine de $36 000 Km$.

Ils tournent dans le même sens que la Terre.

Ils ont une période de révolution d’un jour sidéral, soit $86 164 s$.

V- L'impesanteur

Un objet ou une personne en état d'impesanteur paraissent ne plus être soumis aux effets de la pesanteur.

L’impesanteur se produit dans les véhicules spatiaux satellisés autour de la Terre :

Le centre d’inertie du véhicule spatial et le centre d’inertie du cosmonaute ont la même accélération : $\overrightarrow{a}=\frac{G.M_T}{R^2}\overrightarrow{n}$

Le cosmonaute ne ressent plus la pesanteur, car il a le même mouvement que sa cabine. Il semble « flotter ».

VI- Exercices

6-1/ Exercice 1

On peut imaginer une base relais (pour le matériel comme pour les communications avec la Terre) sur Phobos, un des satellites de Mars.

Dans cette première partie, nous allons étudier le mouvement de ce satellite.

On supposera que tous les objets étudiés sont à répartition sphérique de masse.

Données :

• $G = 6,67.{10}^{-11}N.m^2.k{g}^{-2}$
• Masse de Mars : $m_M=6,42.{10}^{23}kg$
• Distance entre le centre de Mars et celui de Phobos : $r=9,38.{10}^{3}km$
• La masse de Phobos sera notée mP Période de rotation de Mars : $T_M=24h37min$

On supposera que Phobos a un mouvement circulaire uniforme autour de Mars de vitesse v et on supposera que l’on travaille dans un référentiel galiléen centré sur Mars.

1. Donner la définition d’un mouvement circulaire uniforme.

2. Représenter le point d’application, la direction et le sens du vecteur accélération de Phobos sur un schéma.

3. Donner l’expression (sans justification) de la norme du vecteur accélération de Phobos en fonction de $v$ et $r$.

4. Appliquer la deuxième loi de Newton à ce satellite.

5. En déduire que l’expression de sa vitesse de révolution autour de Mars est $\nu =\sqrt{G\frac{m_M}{r}}$

6. Déterminer l’expression reliant $v$, $r$ et $T_P$ (période de révolution de Phobos autour de Mars).

7. Montrer que : $\frac{T_2}{r_3}=9, 22.{10}^{-13}{s}^2.m^{-3}$. En déduire la valeur de $T_P$.

8. Dans quel plan faut-il placer un satellite pour qu’il soit immobile par rapport à la base relais sur Mars ? Justifier votre réponse sans calcul, Quelle est la période $T_S$ de révolution d’un tel satellite ?

VI- Exercices

6-2/ Exercice 2

Zarke AL Yamama est un satellite marocain qui a pour fonction de surveiller les frontières du royaume, de communiquer et de télédétection. Ce satellite a été réalisé par les experts du centre royal de télédétection spatial avec l’aide d’experts internationaux.

Le satellite a été mis en orbite le 10 décembre 2001 à une altitude $h$ de la surface de la Terre, il effectue environ 14 tours par jour autours de la Terre.

On suppose que la trajectoire de $\left(S\right)$ est circulaire, et on étudie son mouvement dans le référentiel géocentrique :

On suppose que la Terre a une symétrie sphérique de répartition de masse.

On néglige les dimensions de $\left(S\right)$ devant la distance qui le sépare du centre de la Terre.

Données :

• La constante gravitationnelle : $G=6,67.{10}^{-11}\left(SI\right)$
• Rayon de la Terre : $r_T=6350km$
• Intensité du champ de pesanteur à la surface de la Terre : $g_o=9,8 m.s^{-2}$.
• L’altitude : $h=1000km$.
• $\overrightarrow{u_{TS}}$ : vecteur unitaire dirigé de $O$ vers $S$.

1. Recopier le schéma de la figure et représenter dessus le vecteur vitesse $\overrightarrow{V_S}$ du satellite $\left(S\right)$ et la force d’attraction universelle appliquée par la Terre sur $\left(S\right)$.

2. Donner l’expression vectorielle de la force exercée par la Terre sur $\left(S\right)$.

3. Écrire dans la base de frenet, l’expression du vecteur accélération du mouvement de $\left(S\right)$.

4. En appliquant la deuxième moi de Newton sur le centre d’inertie du satellite $\left(S\right)$, montrer que le mouvement de $\left(S\right)$ est circulaire uniforme.

5. Écrire l’expression de $V_S$ en fonction de $g_o$, $r_T$ et $h$ et calculer sa valeur.

6. Montrer que la masse de la Terre est $M_T\approx 6.{10}^{24}kg$.

7. Montrer que le satellite $\left(S\right)$ n’est pas ixe par rapport à un observateur terrestre.

Un satellite $(S\text{'})$ tourne autours de la Terre à la vitesse angulaire ω et apparaît ixe par rapport à un observateur terrestre et envoie des photos utilisées en météorologie.

8. Démontrer la relation : ${\omega }^2.{(r_T+z)}^3=Cte$ ; avec $z$ la distance entre la surface de la Terre et le satellite.

9. Trouver la valeur de $z$.

VI- Exercices

6-3/ Exercice 3

La planète Mars est l’une des planètes du système solaire qu’on peut détecter facilement dans le ciel à cause de sa luminosité et de sa couleur rouge. Il possède deux satellites naturels qui sont : Phobos et Deïmos :

Les savants se sont intéressé à son étude depuis longtemps, et on envoyé plusieurs sondes spatiales pour son exploration ce qui a permis d’avoir d’importantes informations sur lui.

Cet exercice propose la détermination de quelques grandeurs physiques concernant cette planète.

Données :

• Masse du Soleil : $M_S=2.{10}^{30}kg$.
• Rayon de Mars : $R_M=6300km$.
• La constante gravitationnelle : $G=6,67.{10}^{-11}\left(SI\right)$.
• La période de la rotation de Mars autours du Soleil : $T_M=687jours$ ; $1jour=86400s$.
• Intensité de la pesanteur à la surface de la Terre : $g_o=9,8N.k{g}^{-1}$.

On considère que Mars et le Soleil ont une symétrie sphérique de répartition de la masse.

Détermination du rayon de la trajectoire de Mars et sa vitesse

On considère que le mouvement de Mars dans le référentiel héliocentrique est circulaire, sa vitesse est $V$ et son rayon est $r$ (on néglige les dimensions de Mars devant les distances le séparant du centre du Soleil et on néglige aussi les autres forces exercées sur lui devant l’attraction universelle exercée par le Soleil).

1. Représenter sur un schéma la force exercée par le Soleil sur Mars.

2. Écrire en fonction de $G$, $M_S$, $M_M$ et $r$, l’expression de l’intensité $F_{S/M}$ de la force d’attraction universelle exercée par le Soleil sur Mars. ($M_M$ est la masse de Mars)

3. En appliquant la deuxième loi de newton, montrer que le mouvement de Mars est circulaire uniforme.

4. En appliquant la deuxième loi de newton, montrer que la relation entre la période et le rayon est : $\frac{{T_M}^2}{r^3}=\frac{4{\pi }^2}{G. M_S}$. et que la valeur de $r$ est : $r\approx 2,3.{10}^{11}m$.

4. Trouver la vitesse $V$.

Détermination de la masse de Mars et l’intensité de la pesanteur à sa surface

On considère que le satellite Phobos est en mouvement circulaire uniforme autours de Mars à la distance $z=6000km$ de sa surface.

La période de ce mouvement est $T_P=460min$ (on néglige les dimensions de Phobos devant les autres dimensions).

5. En étudiant le mouvement de Phobos dans un référentiel dont l’origine est confondue avec le centre de Mars, et qu’on suppose galiléen, trouver la masse $M_M$ de Mars.

6. Trouver l’intensité de la pesanteur $g_{oM}$ à la surface de Mars, et comparer la avec la valeur avec $g_{Mexp}=3,8N.k{g}^{-1}$ mesurée à sa surface moyennant des appareils sophistiqués.