Séance 12 - Repère dans le plan

Sommaire

I- Les coordonnées d’un point

1-1/ Repère Orthonormé du Plan

1-2/ Coordonnées d’un point

1-3/ Coordonnées du milieu d’un segment

II- Les coordonnées d’un vecteur

2-1/ Propriété 1

2-2/ Propriété 2

2-3/ Propriété 3

III- La distance entre deux points

IV- Exercices

4-1/ Exercice 1

4-2/ Exercice 2

4-3/ Exercice 3

4-4/ Exercice 4

4-5/ Exercice 5

4-6/ Exercice 6

4-7/ Exercice 7

I- Les coordonnées d’un point

1-1/ Repère Orthonormé du Plan

Un repère orthonormé est un ensemble de deux axes gradués avec la même unité $(OI=OJ=1unité)$, perpendiculaires et ayant la même origine.

On le note $(O;I;J)$.

La droite $\left(OI\right)$ est appelée l'axe des abscisses.
La droite $\left(OJ\right)$ est appelée l'axe des ordonnées.
Le point $O$ est appelé l'origine du repère.

Dans ce cours le Plan est rapporté à un repère orthonormé $(O;I;J)$ :

I- Les coordonnées d’un point

1-2/ Coordonnées d’un point

Définition

Soit un repère orthonormé $(O;I;J)$.

Tout point $M$ du plan est repéré par un unique couple de réels $(x_M;y_M)$.

Ce couple $(x_M;y_M)$ est appelé coordonnées du point $M$.

• $x_M$ : L’abscisse du point $M$.
• $y_M$ : L’ordonnée du point $M$.

I- Les coordonnées d’un point

1-2/ Coordonnées d’un point

Remarque importante

Si le plan est rapporté à un repère orthonormé $(O;I;J)$, alors :

$O(0;0) ; I(1;0) ; J(0;1)$

Si $M$ appartient à l’axe des abscisses alors son ordonné est nul. On écrit : $M(x_M;0)$

Si $M$ appartient à l’axe des ordonnées alors son abscisse est nul. On écrit : $M(0;y_M)$

I- Les coordonnées d’un point

1-3/ Coordonnées du milieu d’un segment

Dans un repère $(O;I;J)$, on considère les points $A\left(x_A;y_A\right)$ et $B\left(x_B;y_B\right)$.

Si $K$ est le milieu du segment $\left[AB\right]$ alors :

$K\left(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}\right)$

II- Les coordonnées d’un vecteur

2-1/ Propriété 1

Dans un plan rapporté à un repère $(O;I;J)$, on considère les points $A\left(x_A;y_A\right)$ et $B\left(x_B;y_B\right)$.

Les coordonnées du vecteur $\overrightarrow{AB}$ sont : $\left(x_B-x_A;y_B-y_A\right)$

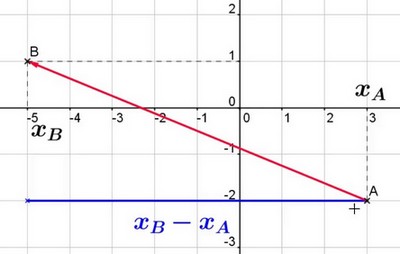
Exemples

II- Les coordonnées d’un vecteur

2-2/ Propriété 2

Deux vecteurs sont égaux si et seulement si ils ont les mêmes coordonnées.

Si $\overrightarrow{DC}=\overrightarrow{AB}$ alors $\left\{\begin{array}{l}{x}_C-x_D=x_B-x_A\\ y_C-y_D=y_B-y_A\end{array}\right.$

Exemples

II- Les coordonnées d’un vecteur

2-3/ Propriété 3

Si $\overrightarrow{AB}(x;y)$ et $\overrightarrow{CD}(x\text{'};y\text{'})$ Alors $\overrightarrow{AB}+\overrightarrow{CD}(x+x\text{'};y+y\text{'})$

Soit $k$ un nombre réel, $\overrightarrow{kAB}$ a pour coordonnées $(kx;ky)$.

Exemples

III- La distance entre deux points

Propriété

Dans un repère orthonormé, soient $E\left(x_E;y_E\right)$ et $F\left(x_F;y_F\right)$.

Alors, la distance entre $E$ et $F$ est donnée par :

$EF=\sqrt{{\left(x_F-x_E\right)}^2+{\left(y_F-y_E\right)}^2}$

Conséquence

Si $\overrightarrow{AB}(x;y)$, alors $AB=\sqrt{x^2+y^2}$

Exemples

IV- Exercices

4-1/ Exercice 1

On considère les points :

$$\begin{gathered} A(-2;3) , B\{5;1\left) \\ C\right(-6,5;-2) , D(-8;-3,2\left) \\ E\right(\frac{2}{3};\frac{5}{2}) , F(-\frac{1}{4};-\frac{7}{4}\left) \\ G\right(11;-\sqrt{3}) , H(-4;\sqrt{12}) \end{gathered}$$

1. Calculer les coordonnées des vecteurs :

$\overrightarrow{AB} ; \overrightarrow{CD} ; \overrightarrow{EF} ; \overrightarrow{GH} ; \overrightarrow{CB} ; \overrightarrow{FD}$

IV- Exercices

4-2/ Exercice 2

On considère un repère du plan.

1. Dans chacun des cas, déterminer les coordonnées du milieu $I$ de $\left[AB\right]$ :

$$\begin{gathered} a) A(1;-5) et B(3;-9) \\ b) A(-2;1) et B(2;0) \\ c) A(-3; \sqrt{2}) et B(2;- \sqrt{2}) \end{gathered}$$

2. Calculer les coordonnées du point $B$ tel que $I$ est le milieu du segment $\left[AB\right]$ :

$$\begin{gathered} a) A(2;-3) et I(4;3\left) \\ b\right) A(-1;-2) et I(5;0) \end{gathered}$$

IV- Exercices

4-3/ Exercice 3

Dans un repère orthonormé du pian, on considère les points $A(4;1)$, $B(0;4)$ et $C(-6;-4)$

1. Calculer $AB$, $AC$ et $BC$.

2. En déduire que le triangle $ABC$ est rectangle.

3. Trouver les coordonnées du centre du cercle circonscrit à ce triangle. Quel est son rayon ?

IV- Exercices

4-4/ Exercice 4

Dans le plan muni d’un repère orthonormé, on considère les points $A(6;3)$, $B(3;2)$ et $C(7;0)$.

1. Construire les points $A$, $B$ et $C$.

2. Déterminer le couple de coordonnées des vecteurs $\overrightarrow{AB}$, $\overrightarrow{AC}$ et $\overrightarrow{BC}$.

3. Calculer les distances $AB$, $AC$ et $BC$.

4. Montrer que le triangle $ABC$ est isocèle et rectangle en $A$.

On considère le point $D(4;-1)$.

5. Construire le point $D$.

6. Montrer que les segments $\left[AD\right]$ et $\left[BC\right]$ ont le même milieu.

7. En déduire la nature du quadrilatère $ABCD$.

IV- Exercices

4-5/ Exercice 5

Dans un repère orthonormé, on considère les points $A(3;4)$, $B(3;-2)$ et $C(-4;-2)$.

1. Tracer la figure.

2. Déterminer la nature du triangle $ABC$.

3. Calculer les coordonnées du point $K$ le centre du cercle circonscrit du triangle $ABC$.

4. Déterminer les coordonnées du point $D$ l'image de $B$ par la translation de vecteur $\overrightarrow{AC}$.

5. Calculer les coordonnées du point E tel que : $\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BE}$.

6. Montrer que le point $C$ est le milieu de $\left[DE\right]$.

7. Calculer les coordonnées du point $N$ tel que : $\overrightarrow{AN}=-3\overrightarrow{AB}$.

8. Calculer les coordonnées du point $F$ point d’intersection de la droite $\left(AB\right)$ et l’axe des abscisses.

IV- Exercices

4-6/ Exercice 6

On considère les points $A(4;1)$ ; $B(2;3)$ ; $C(-1;0)$ et $D\left(1;-2\right)$.

1. Montrer que $ABCD$ est un parallélogramme.

2. Calculer les distances $AB$, $AC$ et $BC$.

3. Montrer que $ABCD$ est un rectangle.

IV- Exercices

4-7/ Exercice 7

On considère les points $A\left(1;2\right)$ ; $B\left(3;1\right)$ ; $C(-1;1)$ et $D\left(1;0\right)$.

1. Quelle est la nature du triangle $ABC$ ?

2. Comparer les vecteurs $\overrightarrow{AC}$ et $\overrightarrow{BD}$.

3. Montrer que $ABDC$ est un losange.

4. Calculer les coordonnées du point $E$ tel que $\overrightarrow{CE}=\frac{5}{2}\overrightarrow{CD}$.