Séance 19B - Mouvements plans : Particule chargée dans un champ magnétique

Sommaire

I- Mouvement d'une particule chargée dans un champs magnétique uniforme

1-1/ Le champ magnétique uniforme

1-2/  Déviation d'une particule chargée dans un champ magnétique uniforme

1-3/  La force magnétique (force de Lorentz)

1-4/ Étude du mouvement d'une particule chargée dans un champ magnétique uniforme

1-5/ La déviation magnétique

II- Exercices

2-1/ Exercice 1

2-2/ Exercice 2

2-3/ Exercice 3

2-4/ Exercice 4

I- Mouvement d'une particule chargée dans un champs magnétique uniforme

1-1/ Le champ magnétique uniforme

Un champ magnétique est dit uniforme s'il est constant en direction, en sens et en valeur.

• Exemple : Le champ magnétique est uniforme entre les bobines d'Helmholtz parcourues par un courant électrique :

L'unité de l'intensité du champ magnétique est le tesla (T).

Remarque

Si le vecteur $\overrightarrow{B}$ est perpendiculaire au plan de la feuille et dirigée vers l'avant on le représente par : $\odot \overrightarrow{B}$

Si le vecteur $\overrightarrow{B}$ est perpendiculaire au plan de la feuille et dirigée vers l'arrière on le représente par : $\otimes \overrightarrow{B}$

I- Mouvement d'une particule chargée dans un champs magnétique uniforme

1-2/  Déviation d'une particule chargée dans un champ magnétique uniforme

Expérience

On utilise un tube de crookes (qui contient un canon d'électrons permettant d'obtenir un faisceau d'électrons ayant la même vitesse), à l'intérieur duquel il y'a un champ magnétique uniforme entre deux bobines d'Helmholtz parcourues par un courant électrique :

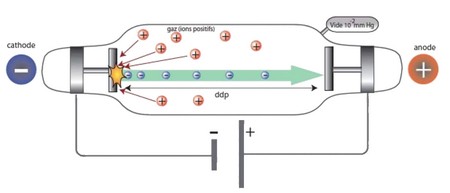
On constate expérimentalement que :

Si la vitesse des électrons $\overrightarrow{v_0}$ est parallèle à $\overrightarrow{B}$, le faisceau d'électrons ne subit pas de déviation.

Si la vitesse des électrons $\overrightarrow{v_0}$ est perpendiculaire à $\overrightarrow{B}$, le faisceau d'électrons dévie et sa trajectoire devient circulaire.

I- Mouvement d'une particule chargée dans un champs magnétique uniforme

1-2/  Déviation d'une particule chargée dans un champ magnétique uniforme

Interprétation

La déviation du faisceau d'électron est due à l'existence d'une force magnétique qui s'exerce sur toute particule chargée et en mouvement dans un champ magnétique uniforme qu'on appelle : force magnétique ou force de Lorentz.

I- Mouvement d'une particule chargée dans un champs magnétique uniforme

1-3/  La force magnétique (force de Lorentz)

Définition

Toute particule chargée de vitesse  est soumise dans un champ magnétique uniforme à une force magnétique appelée force de Lorentz donnée par la relation suivante :

$\overrightarrow{F}=q.\overrightarrow{v}\wedge \overrightarrow{B}$

Le symbole $\wedge$ signifie produit vectoriel.

Caractéristiques de la force magnétique

L'intensité : $F=\left|q\right|.v.B.\sin \left(\widehat{\overrightarrow{B},\overrightarrow{v}}\right)$

La direction : la force magnétique.

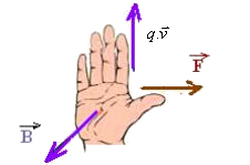
Le sens : il est donné par la règle de la main droite suivante :

En plaçant la main droite tendue de sorte que les doigts soient dirigés dans le sens du produit $q.\overrightarrow{v}$ et la paume de la main soit dirigée dans le sens de $\overrightarrow{B}$, le pouce tendu indique le sens de la force magnétique :

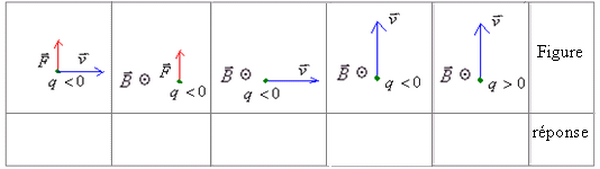
Exemples

I- Mouvement d'une particule chargée dans un champs magnétique uniforme

1-4/ Étude du mouvement d'une particule chargée dans un champ magnétique uniforme

Mouvement uniforme

L'électron dans le champ magnétique est soumis à l'action de la force magnétique $\overrightarrow{F}=q.\overrightarrow{v}\wedge \overrightarrow{B}$, cette force de Lorentz est toujours perpendiculaire au vecteur vitesse $\overrightarrow{v}$.

Donc le produit scalaire $\overrightarrow{F}.\overrightarrow{v}=0$

Par conséquence la puissance de la force magnétique est nulle $P=\overrightarrow{F}.\overrightarrow{v}=0$,donc son travail est nul$W\overrightarrow{F}=0$ .

En appliquant le théorème de l'énergie cinétique : $\Delta E_c=W\overrightarrow{F}=0\Rightarrow E_{c_i}=E_{c_f}$

Donc sa vitesse est constante $v= Cte$.

Donc l'action du champ magnétique ne modifie pas l'énergie cinétique de la particule.

I- Mouvement d'une particule chargée dans un champs magnétique uniforme

1-4/ Étude du mouvement d'une particule chargée dans un champ magnétique uniforme

Mouvement plan

La vitesse de l’électron est constante $v= Cte$.

Donc son accélération tangentielle $a_t=\frac{dv}{dt}=0$ est nulle.

Alors l'accélération de l'électron est normale.

Et on a $\overrightarrow{F}=q.\overrightarrow{v}\wedge \overrightarrow{B}$

Donc la force magnétique $\overrightarrow{F}$ est perpendiculaire au plan $\left(\overrightarrow{B},\overrightarrow{v}\right)$, est elle aussi normale.

En conclusion, le mouvement de l'électron est plan, il se fait dans un plan perpendiculaire au vecteur champ magnétique.

I- Mouvement d'une particule chargée dans un champs magnétique uniforme

1-4/ Étude du mouvement d'une particule chargée dans un champ magnétique uniforme

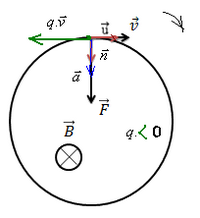
Mouvement circulaire

Dans le repère de Frenet, le vecteur accélération : $\overrightarrow{a}=a_n\overrightarrow{n}+a_t\overrightarrow{u}$

or :$v=Cte\Rightarrow a_t=\frac{dv}{dt}=0$

Donc l'accélération est normale.

En appliquant la deuxième loi de Newton : $\overrightarrow{F}=q.\overrightarrow{v}\wedge \overrightarrow{B}=m\overrightarrow{a_G}$

En projetant sur la normale : $\overrightarrow{F}=\left|q\right|v.B=m\frac{v^2}{R}\Rightarrow \overline{)R=\frac{mv}{\left|q\right|.B}}$

Le rayon est constant donc le mouvement est circulaire.

I- Mouvement d'une particule chargée dans un champs magnétique uniforme

1-5/ La déviation magnétique

On fait pénétrer un faisceau d'électron dans une région de l'espace de largeur $\mathcal{l}$ dans laquelle règne un champ magnétique $\overrightarrow{B}$ uniforme avec une vitesse $\overrightarrow{v_0}$, le faisceau d’électrons est soumis à l'action de la force magnétique et son mouvement devient circulaire de rayon $R=\frac{m{v}_0}{\left|q\right|.B}$ dans le champ magnétique.

Les électron du faisceau quittent le champ magnétique au point $S$ et prennent un mouvement rectiligne uniforme jusqu'à ce qu'ils rencontrent l'écran au point $P$.

On appelle déviation magnétique la distance $D_m=O\text{'}P$

$$\begin{gathered} \left\{\begin{array}{l}\sin \alpha =\frac{\mathcal{l}}{R} \left(HM\text{'}I\right)\\ \tan \alpha =\frac{D_m}{D} \left(JPO\text{'}\right)\end{array}\right. \\ \tan \alpha \approx \sin \alpha \\ \Rightarrow \frac{D_m}{D}=\frac{\mathcal{l}}{R} \\ \Rightarrow \overline{)D_m=\frac{D\mathcal{l}}{R}=\frac{D\mathcal{l}\left|q\right|B}{m{v}_0}} \end{gathered}$$

II- Exercices

2-1/ Exercice 1

Les ions $M{g}^{2+}$ pénètrent dans une région de l’espace où règne un champ magnétique uniforme $\overrightarrow{B}$ (perpendiculaire au plan de la figure). Avec une vitesse $V_0=1,6.{10}^{4}m.s^{-1}$

1. Donner les caractéristique de la force magnétique $\overrightarrow{F_m}$

2. Déterminer le sens du champs magnétique $\overrightarrow{B}$

3. En appliquant la deuxième loi de newton dans un référentiel galiléen, montrer que le mouvement des ions $M{g}^{2+}$ est circulaire uniforme

4. Calcule la masse d’ion $M{g}^{2+}$ (On donne $OM=4cm$)

Données :

• L’intensité du  champs magnétique $B=0,1T$
• La charge élémentaire $e=1,6.{10}^{-19}C$

II- Exercices

2-2/ Exercice 2

On considère les ions de deux isotopes ${}_{80}{}^{200}H{g}^{2+}$ et ${}_{80}{}^{202}H{g}^{2+}$ du mercure.

Ils pénètrent en $A$, avec une vitesse $V$ non nulle, dans une capsule où règne un champ magnétique uniforme (perpendiculaire au plan de la feuille) :

1. Indiquer le sens du champ magnétique pour que les ions soient déviés vers le détecteur $D$.

2. Montrer que dans cette capsule les ions ont un mouvement uniforme, et exprimer les rayons $R$ de la trajectoire de deux isotopes en fonction de $m$, $e$, $v$ et $B$.

3. Déterminer lequel de ces deux ions va être le plus dévié. Justifier.

II- Exercices

2-3/ Exercice 3

Deux particules chargées $H{e}^{2+}$ et $O^{2-}$ sont introduites en un point $A$, avec la même vitesse initiale $\overrightarrow{V}$, dans un espace où règne un champ magnétique uniforme $\overrightarrow{B}$ perpendiculaire au vecteur $\overrightarrow{V}$.

On considère que les deux particules $H{e}^{2+}$ et $O^{2-}$ ne sont soumises qu’à la force de Lorentz.

Données :

L’expression de la force de Lorentz : $\overrightarrow{F}=q\overrightarrow{V}\wedge \overrightarrow{B}$
La masse de la particule $H{e}^{2+}$ : $m\left(H{e}^{2+}\right)=6,68.{10}^{-27}Kg$

La figure suivante représente l’enregistrement des deux trajectoires des particules $H{e}^{2+}$ et $O^{2-}$ dans le champ magnétique uniforme $\overrightarrow{B}$ :

1. Identifier la trajectoire correspondante à chaque particule.

2. En appliquant la deuxième loi de Newton dans un référentiel galiléen, montrer que le mouvement de l’ion $H{e}^{2+}$ est uniforme et de trajectoire circulaire de rayon $R_{H{e}^{2+}}=\frac{m_{H{e}^{2+}}.V}{2.e.B}$

3. En exploitant la figure, déterminer le rapport $\frac{R_{O^{2-}}}{R_{H{e}^{2+}}}$

4. Montrer que la masse de la particule $O^{2-}$ est $m\left(O^{2-}\right)=2,67.{10}^{-26}Kg$