
Physique et Chimie : 2ème Année Bac
Séance 17 (Les lois de Newton)
Professeur : Mr El GOUFIFA Jihad
Sommaire
I- Complément mathématique
1-1/ Notions générales sur le mouvement
1-2/ Vecteur vitesse
1-3/ Vecteur accélération
1-4/ Repère de Frenet
II- Le Mouvement
2-1/ Mouvement rectiligne uniforme
2-2/ Mouvement rectiligne uniformément varié
III- Les forces intérieures et les forces extérieures
IV- Les lois de Newton
4-1/ La 1ère loi de Newton (Principe d’inertie)
4-2/ La 2ème loi de Newton (Théorème de centre d’inertie)
4-3/ La 3ème loi de Newton (Principe des actions réciproques)
V- Applications
5-1/ Mouvement sur un plan horizontal sans frottement
5-2/ Mouvement sur un plan horizontal avec frottement
5-3/ Mouvement sur un plan incliné sans frottement
5-4/ Mouvement sur un plan incliné avec frottement
5-5/ Mouvement curviligne
VI- Exercices
6-1/ Exercice 1
6-2/ Exercice 2
6-3/ Exercice 3
6-4/ Exercice 4
I- Complément mathématique
1-1/ Notions générales sur le mouvement
Nous savons que le mouvement d'un corps est relatif au référentiel choisi, c'est-à-dire que les corps ne se déplacent que par rapport à d'autres corps.
Donc pour étudier le mouvement d'un corps on doit choisir un solide de référence fixe appelé référentiel puis un repère d'espace et un repère de temps liés à ce référentiel.
La plupart des temps, on choisi comme référentiel d'étude le référentiel terrestre.
Pour repérer la position du mobile, on utilise un repère d'espace .
Le vecteur position permet de repérer le point dans l’espace par rapport à un référentiel choisi pour l’étude.
Les fonctions , et sont les équations horaires du mouvement.
I- Complément mathématique
1-2/ Vecteur vitesse
Le vecteur vitesse instantanée du centre d'inertie d'un corps est égal à la dérivée du vecteur position par rapport au temps :
Le module du vecteur vitesse est en .
I- Complément mathématique
1-3/ Vecteur accélération
Le vecteur accélération du centre d'inertie d'un corps est égal à la dérivée du vecteur vitesse par rapport au temps :
Le module du vecteur accélération est en .
I- Complément mathématique
1-4/ Repère de Frenet
Le repère de Frenet est un repère local orthonormé lié au mobile que l'on note .
Le vecteur unitaire est tangent à la trajectoire au point et orienté dans le sens du mouvement.
Le vecteur unitaire est normal, et dirigé vers le centre de courbure de la trajectoire, il est perpendiculaire à :
L'expression du vecteur accélération dans le repère de Frenet est :
- est la composante tangentielle du vecteur accélération.
- est la composante normale du vecteur accélération.
est le rayon de courbure de la trajectoire au point
Si la trajectoire est un cercle (Rayon du cercle).
II- Le Mouvement
2-1/ Mouvement rectiligne uniforme
Le mouvement rectiligne uniforme est caractérisé par :
- Une trajectoire rectiligne.
- Une vitesse constante : .
- Une accélération nulle : .
L'équation horaire du mouvement est : ( : abscisse à l'origine).
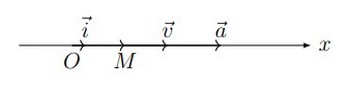
II- Le Mouvement
2-2/ Mouvement rectiligne uniformément varié
Le mouvement rectiligne uniformément varié est caractérisé par :
- Une trajectoire rectiligne.
- Une accélération constante
L'équation de la vitesse est .
L'équation horaire du mouvement est .
Dans ce cas la vitesse en fonction du temps est une fonction affine, son coefficient directeur est égal à l'accélération.
 |
 |
 |
III- Les forces intérieures et les forces extérieures
On appelle forces extérieures, les forces qui s'exercent sur le système par des corps qui n'appartiennent pas au système.
On appelle forces intérieures, les forces qui s'exercent sur le système par des corps qui appartiennent pas au système.
Un système est dit isolé s'il n'est soumis à aucune force extérieure.
Un système est dit pseudo-isolé si les force extérieure auquel il est soumis se compensent.
IV- Les lois de Newton
4-1/ La 1ère loi de Newton (Principe d’inertie)
Dans un référentiel galiléen, tout corps isolé (aucune force n’est appliquée) ou pseudo isolé (la somme des forces est nulle) est soumis d’un mouvement rectiligne uniforme e ou il est immobile ⃗.
Remarque
Le repère de Copernic est le meilleur repère galiléen (son origine est le soleil et ses trois axes son dirigés vers trois étoiles fixes).
Tout repère en mouvement de translation rectiligne uniforme par rapport au repère de Copenic est considéré galiléen, donc tous les repères terrestres peuvent être considérés galiléen pendant des intevalles de temps courts.
IV- Les lois de Newton
4-2/ La 2ème loi de Newton (Théorème de centre d’inertie)
Dans un repère galiléen la somme des vecteurs forces qui s'exercent sur un corps est égale au produit de la masse du corps et du vecteur accélération de son centre d'inertie.
IV- Les lois de Newton
4-3/ La 3ème loi de Newton (Principe des actions réciproques)
Lorsqu’il y a une interaction entre deux corps et , le corps exerce une force sur le corps B, on la note , et le corps exerce une force de même intensité .
Ces deux vecteurs sont liés vectoriellement par la relation suivante :
Leur intensité est :
est la constante de gravitation universelle, elle vaut , et d la distance qui les sépare.
V- Applications
5-1/ Mouvement sur un plan horizontal sans frottement
On considère un corps solide en mouvement sur un plan horizontal sans frottement sous l’action d’une force constante comme l’indique la figure suivante :

V- Applications
5-2/ Mouvement sur un plan horizontal avec frottement
On considère un corps solide en mouvement sur un plan horizontal avec frottement sous l’action d’une force constante comme l’indique la figure suivante :

V- Applications
5-3/ Mouvement sur un plan incliné sans frottement
On libère un corps solide de masse sur un plan incliné d’un angle par rapport à l’horizontale et il glisse sans frottement vers le bas :
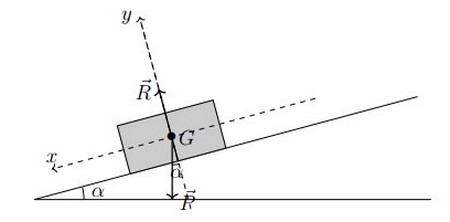
V- Applications
5-4/ Mouvement sur un plan incliné avec frottement
On tire un corps solide de masse sur un plan incliné d’un angle par rapport à l’horizontale en utilisant une corde, il glisse avec frottement vers le haut :

V- Applications
5-5/ Mouvement curviligne
Une bille de masse se déplace sur un un rail , contenant trois portions, comme l’indique la figure suivante :

- La portion est inclinée d’une angle où le mouvement se fait sans frottement :

- La portion horizontale où le mouvement se fait avec frottement :

- La portion est circulaire de rayon , le mouvement se fait sans frottement :
VI- Exercices
6-1/ Exercice 1
Les coordonnées du vecteur position au cours du mouvement d’un corps solide dans un repère orthonormé sont :
- Trouver l’équation de la trajectoire . En déduire sa nature.
- Déterminer les coordonnées du vecteur vitesse dans le repère .
- Calculer la norme de la vitesse à la date .
- Trouver les coordonnées du vecteur accélération dans le repère .
- Calculer la norme du vecteur accélération .
- Déterminer la nature du mouvement du mobile (accéléré ou retardé).
VI- Exercices
6-2/ Exercice 2
Un skieur (avec ses équipements) assimilé à un corps solide de masse , décrit une piste formée par deux parties :
- , une pente inclinée de avec le plan horizontal
- , une voie rectiligne et horizontale.
Le contact entre le skieur avec ses équipements se fait sans frottements sur la partie :
L’intensité de gravitation .
On étudie le mouvement du corps dans un repère galiléen .
La partie
- En appliquant la 2ème loi de Newton, déterminer l’abscisse du vecteur accélération du centre d’inertie de . Quelle est la nature de son mouvement ?
- Déterminer les équations horaires et du mouvement, on prend comme origine des dates lorsque le skieur est au point et sa vitesse initiale est nulle.
- Déterminer l’instant ou le corps atteint le point .
- Calculer la vitesse du skieur au point .
- Calculer l’intensité de la réaction du plan sur le skieur.
La partie
Le solide arrive au point avec la vitesse .
On prend comme origine des dates et d’espace lorsque le skieur atteint le point .
Le contact entre le plan et se fait avec frottements équivalents à une force constante et horizontale et de sens opposé à celui du mouvement.
- En appliquant la 2ème loi de Newton, déterminer l’abscisse du vecteur accélération
- Déterminer les équations horaires et du mouvement.
- Déterminer l’instant tC sachant que arrête au point .
- Calculer la distance .
- Calculer l’intensité de la réaction du plan sur le skieur.
- En déduire le coefficient de frottement et l’angle de frottement .
VI- Exercices
6-3/ Exercice 3
Une piste dans un plan vertical est constituée d’une partie horizontale de longueur et d’une partie CD circulaire de rayon .
On lance , à , un corps de masse à partir du point origine de repère considéré galiléen avec une vitesse initiale et le corps se déplace sur la partie avec frottement :
On prend .
- Trouver l’expression de la force de frottement , calculer sa valeur sachant que l’accélération du centre d’inertie est .
- Calculer la valeur de la réaction de la partie sur le corps . Déduire la valeur de l’angle de frottement.
- En utilisant les équations horaires et déterminer la vitesse au point .
Arrivant au point , le corps continue son mouvement sur la partie circulaire sans frottement .
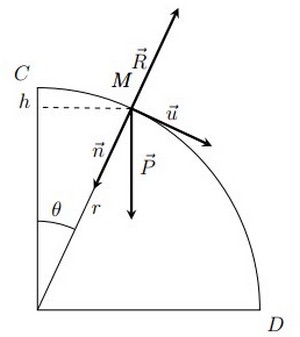
- Trouver l’expression de la force de réaction appliquée par la partie sur le corps à la position repérée par l’angle en fonction de , , , et la vitesse au point .
- Appliquer le théorème de l’énergie cinétique entre et et montrer que l’expression de s’écrit : .
6)Déterminer la valeur de l’angle maximal pour lequel le solide revient dans le sens inverse .
- Calculer l’intensité de la force de réaction à cet angle.
Rappel
Dans le repère de Frenet, le vecteur accélération s’écrit : avec et .
VI- Exercices
6-4/ Exercice 4
Cet exercice se propose d’étudier le mouvement du centre d’inertie d’un système formé d’un motard et d’une moto se déplaçant sur une piste de compétition.
Cette piste est formée d’une partie rectiligne inclinée d’un angle p par rapport à l’horizontale
Dans tout l’exercice, les frottements sont négligés et l’étude du mouvement du centre d’inertie est réalisée dans le référentiel terrestre considéré comme galiléen.
Données :
- L’angle
- Intensité de la pesanteur :
- Masse du système : m =190 kg.
À un instant choisi connue origine des dates , le système s’élance sans vitesse initiale, d’une position où le centre d’inertie est confondu avec le point .
Le système est soumis, au cours de son mouvement sur la partie , à la réaction du plan incliné, à son poids et à une force motrice constante, dont la ligne d’action est parallèle à la trajectoire de et le sens est celui du mouvement.
Pour étudier le mouvement de au cours de cette phase, on choisit un repère d’espace parallèle à et on repère la position de par son abscisse :
- En appliquant la deuxième loi de Newton, montrer que l’expression de l’accélération du mouvement de est
La courbe suivante représente les variations de la vitesse instantanée du centre d’inertie en fonction du temps :
- En exploitant cette courbe, trouver la valeur de l’accélération .
- Déduire l’intensité de la force motrice.
- Écrire l’expression numérique de l’équation horaire du mouvement de .
- Sachant que , déterminer l’instant de passage de par le point .
- Calculer la vitesse de passage de par le point .


