
Mathématiques : Tronc Commun
Séance 9 (Trigonométrie 1 - Règles du calcul trigonométrique)
Professeur : Mr ETTOUHAMY Abdelhak
Sommaire
I- Cercle trigonométrique
1-1/ Définition
1-2/ Remaque
1-3/ Abscisses curvilignes
II- Angle orienté de deux demi-droites – de deux vecteurs non nuls
2-1/ Radian – grade
2-2/ Mesure d’un angle orienté de deux demi-droites
2-3/ Angle déterminé par deux vecteurs non nuls
III- Lignes trigonométriques du réel
IV- Signe de et et
4-1/ Quadrant d’un cercle
4-2/ Signes des lignes trigonométriques
4-3/ Angles remarquables
V- Relations entre les angles
5-1/ Angles opposés
5-2/ Angles supplémentaires
5-3/ Angles opposés supplémentaires
5-4/ Angles complémentaires
5-5/ Angles opposés complémentaires
5-6/ Résumé des formules précédentes
VI- Exercices
6-1/ Exercice 1
6-2/ Exercice 2
6-3/ Exercice 3
6-4/ Exercice 4
I- Cercle trigonométrique
1-1/ Définition :
Tout cercle du plan (P) tel que :
- que son rayon est .
- qui est muni d’un origine .
- qui est orienté positif ( qui est le sens contraire de la rotation des aiguilles du montre ).
Ce cercle est appelé cercle trigonométrique.
Si tous les cercles du plan sont orientés d’une orientation positive, on dit que le plan est orienté positif (ou direct).

I- Cercle trigonométrique
1-2/ Remarque
Si le plan est rapporté a un repère orthonormé et est le centre du cercle et le point est placé dans le sens positif, on dit que le cercle trigonométrique est lié au repère orthonormé (avec et ).
Pour tout le cours : le cercle est le cercle trigonométrique d’origine et son centre est le point .

I- Cercle trigonométrique
1-3/ Abscisses curvilignes
est un point de , il existe un et un seul abscisse curviligne de qui appartienne à ( c.à.d. ). Cet abscisse est appelé abscisse curviligne principal de .
Si est situé sur le demi cercle «supérieure», la mesure principale appartienne à , sinon la mesure principale appartienne à .
Les abscisses curvilignes de sont , donc l’abscisse curviligne principale de est .
Les abscisses curvilignes de sont , donc l’abscisse curviligne principale de est .
Les abscisses curvilignes de sont , donc l’abscisse curviligne principale de est .
Les abscisses curvilignes de sont , donc l’abscisse curviligne principale de est .

II- Angle orienté de deux demi-droites – de deux vecteurs non nuls
2-1/ Radian – grade
Définition
et deux points du cercle trigonométrique d’origine et son centre est le point et M un point de .
- La longueur de l’arc géométrique IM intercepte par l’angle géométrique IOM est la mesure de IOM en radian et se note rad ou rd.
- la mesure d’un angle plat en radian est égale à
- la mesure d’un angle droit en radian est égale à
Remarque
Il existe une autre unité de mesure des angles, on l’appelle grade
On la note par tel que et
Si la mesure d'un angle est et et respectivement en degré et radian et grade, alors .
Exemple
II- Angle orienté de deux demi-droites – de deux vecteurs non nuls
2-2/ Mesure d’un angle orienté de deux demi-droites
Définition 1
Soit et deux demi droites du plan tel que et .
Le couple est appelé l’angle orienté du demi-droites, on le note .
Le couple détermine un autre angle orienté, on le note qui est différent de l’angle .
Définition 2
On considère dans le plan deux points et puis le cercle trigonométrique de centre tel que et .
Les deux demi-droites et coupent respectivement en et tel que leurs abscisses curvilignes sont et . On a :
- Les mesures de l’angle orienté sont les nombres réels ,
On note ou encore .
On lit : mesures de l’angle orienté congrue à modulo .
- La mesure qui vérifie s’appelle la mesure principale de l’angle orienté .
Exemple
II- Angle orienté de deux demi-droites – de deux vecteurs non nuls
2-2/ Mesure d’un angle orienté de deux demi-droites
Propriété
Le plan est orienté positif, est un point de .
Soient et et trois demi-droites de .
On a :
: Relation de chasles
Exemple
II- Angle orienté de deux demi-droites – de deux vecteurs non nuls
2-3/ Angle déterminé par deux vecteurs non nuls
Définition
Le plan est orienté positif, est un point de .
Soient et deux vecteurs non nuls de .
Soient et deux points de tel que et .
L’angle orienté des vecteurs et est l’angle orienté (c.à.d. des deux demi-droites et , on le note .
Les mesures de l’angle orienté sont appelées les mesures de l’angle orienté , on note .
On a :
La mesure de l’angle orienté qui appartienne à est appelée la mesure principale de .
Exemple
II- Angle orienté de deux demi-droites – de deux vecteurs non nuls
2-3/ Angle déterminé par deux vecteurs non nuls
Propriété
Le plan est orienté positif, est un point de .
Soient et et trois vecteurs non nuls de .
On a :
Exemple
III- Lignes trigonométriques du réel
Définition
est une abscisse curviligne du point tel que est le cercle trigonométrique d’origine lié au repère orthonormé.
par rapport au repère orthonormé direct.
Le réel (abscisse de ) est appelé le sinus du réel , on le note , d’où .
Le réel (ordonnée de ) est appelé le cosinus du réel , on le note , d’où .
Le réel (abscisse du point ) est appelé la tangente du réel , on le note , d’où (sachant la droite est tangente au cercle en et ).

III- Lignes trigonométriques du réel
Conséquences

IV- Signe de et et
4-1/ Quadrant d’un cercle
On divise le cercle en quatre arcs de même longueur suivant le sens positif.
x est une abscisse curviligne du point .
Le 1er arc : si on dit que est situé dans le premier quadrant.
Le 2ème arc : si on dit que est situé dans le deuxième quadrant.
Le 3ème arc : si on dit que est situé dans le troisième quadrant.
Le 4ème arc : si on dit que est situé dans le quatrième quadrant
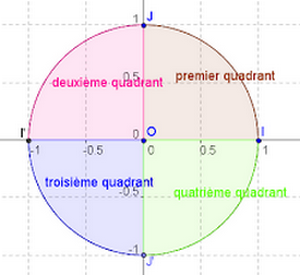
IV- Signe de et et
4-2/ Signes des lignes trigonométriques




IV- Signe de et et
4-3/ Angles remarquables
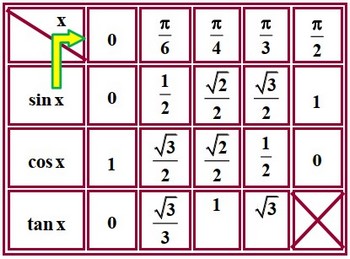

V- Relations entre les angles
5-1/ Angles opposés

V- Relations entre les angles
5-2/ Angles supplémentaires

V- Relations entre les angles
5-3/ Angles opposés supplémentaires

V- Relations entre les angles
5-4/ Angles complémentaires
V- Relations entre les angles
5-5/ Angles opposés complémentaires

V- Relations entre les angles
5-6/ Résumé des formules précédentes

VI- Exercices
6-1/ Exercice 1
Soit un cercle trigonométrique et un repère orthonormé direct lié avec .
- Déterminer l’abscisse curviligne principale de chacun des points suivants :
- Déterminer la mesure principale des angles orientés suivants :
- Placer les points , et dans le cercle trigonométrique .
VI- Exercices
6-2/ Exercice 2
Soit .
- Exprimer en fonction de et :
- Calculer , et .
VI- Exercices
6-3/ Exercice 3
- Résoudre dans l’intervalle les inéquations suivantes :
VI- Exercices
6-4/ Exercice 4
Pour tout , on pose :
- Montrer que :
- Résoudre dans l’équation :
- Résoudre dans l’intervalle l’inéquation :


