Séance 21 - Le champ magnétique

Sommaire

I- Les aimants

1-1/ Définition d’un aimant

1-2/ Pôles d’un aimant

II- Mise en évidence du champ magnétique

2-1/ Action d’un aimant sur une aiguille aimantée

2-2/ Action d’un courant électrique sur une aiguille aimantée

III- Champ magnétique et spectres magnétiques

3-1/ Vecteur champ magnétique

3-2/ Mesure des champs magnétiques

3-3/ Spectre magnétique et lignes de champs magnétiques

3-4/ Champ magnétique uniforme

3-5/ Superposition de champs magnétiques

IV- Champ magnétique terrestre

V- Exercices

5-1/ Exercice 1

5-2/ Exercice 2

5-3/ Exercice 3

5-4/ Exercice 4

I- Les aimants

1-1/ Définition d’un aimant

L'aimant est un corps qui a la propriété d’attirer les métaux ferreux.

Ils existent naturellement dans la nature, mais on les fabrique artificiellement.

Ils sont généralement en acier dur (cobalt).

I- Les aimants

1-2/ Pôles d’un aimant

Un aimant comporte toujours deux pôles appelés le pôle nord (N) et le pôle sud (S) situés, en général, aux deux extrémités.

Les pôles d’un aimant sont inséparables.

Un aimant exerce une action à distance sur un autre aimant :

• Deux pôles identiques se repoussent.
• Deux pôles différents s’attirent.

II- Mise en évidence du champ magnétique

2-1/ Action d’un aimant sur une aiguille aimantée

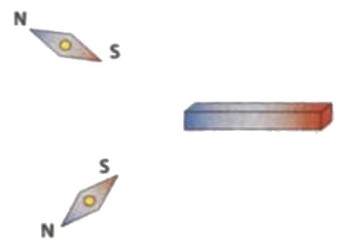
Lorsqu’on place un aimant au voisinage d’une aiguille aimantée, on constate que son orientation change suivant la position de l’aimant.

La présence d’un aiment modifie les propriétés de l’espace qui l’entoure : on dit qu’il crée un champ magnétique dans son environnement.

II- Mise en évidence du champ magnétique

2-2/ Action d’un courant électrique sur une aiguille aimantée

Une aiguille aimantée dévie au voisinage d’un conducteur parcouru par un courant électrique continu. Sa déviation dépend du sens du courant qui traverse le conducteur.

Un courant continu circulant dans un conducteur crée un champ magnétique autour de celui-ci.

III- Champ magnétique et spectres magnétiques

3-1/ Vecteur champ magnétique

Lorsqu’on pose une aiguille aimantée pouvant osciller autour d’un axe vertical, dans un point où règne un champ magnétique noté $\overrightarrow{B}$, elle s’oriente suivant une direction et un sens déterminés.

Par convention le sens de $\overrightarrow{B}$ est celui qui indique le pôle nord de l’aiguille aimantée :

Le vecteur champ magnétique $\overrightarrow{B}$ en un point $M$ a les propriétés mathématiques d’un vecteur :

• Origine : le point $M$
• Direction : celle prise par l’aiguille aimantée placée en $M$
• Sens : celui qui indique le pôle nord de l’aiguille aimantée (du sud vers le nord de l’aiguille)
• Valeur : (mesurée par un tesla-mètre) exprimée en Tesla $\left(T\right)$.

III- Champ magnétique et spectres magnétiques

3-2/ Mesure des champs magnétiques

L’intensité du champ magnétique notée B, s’exprime en teslas (T) du nom d’un physicien américain Nikola Tesla (1856-1943).

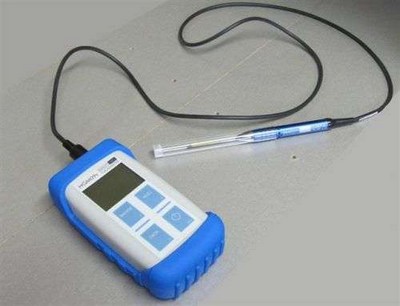
L’appareil permettant de mesurer l’intensité d’un champ magnétique s’appelle le teslamètre.

La valeur d'un champ magnétique en un point dépend de la position de ce point par rapport à la source (ou aux sources) du champ magnétique.

III- Champ magnétique et spectres magnétiques

3-3/ Spectre magnétique et lignes de champs magnétiques

Les lignes de champ magnétique sont des courbes qui sont tangente aux vecteurs champs magnétiques en chacun de ces points. Elles sont orientées dans le sens des vecteurs champs magnétiques.

Chaque ligne de champ est orientée de telle façon qu’elle sorte par le pôle nord (N) et qu’elle rentre par le pôle sud (S).

Le spectre magnétique est l’ensemble des lignes de champ.

Exemples

Remarque

Un champ magnétique est uniforme dans une région de l’espace, si le vecteur champ magnétique garde les mêmes caractéristiques (direction, sens et valeur) en toutes points de cette région, les lignes de champ sont alors des droites parallèles.

III- Champ magnétique et spectres magnétiques

3-4/ Champ magnétique uniforme

Un champ magnétique est uniforme dans une région de l’espace, si le vecteur champ magnétique a les mêmes caractéristiques (directions, sens et valeur) en tout point de cette région.

Le spectre du champ magnétique uniforme est formé de segments de droites parallèles entres eux. C’est le cas dans l’entrefer d’un aimant en U.

III- Champ magnétique et spectres magnétiques

3-5/ Superposition de champs magnétiques

S’il y a plusieurs champs magnétiques (créés par plusieurs sources distinctes), le vecteur champ magnétique résultant en un point est égal à la somme vectorielle des champs créés par chacune des sources en ce point.

IV- Champ magnétique terrestre

Autour de la terre règne un champ magnétique appelé champ géomagnétique.

Le pôle magnétique sud se trouve à proximité du pôle géographique nord, de même le pôle magnétique nord se trouve près du pôle sud géographique.

Le champ magnétique terrestre (ou champ géomagnétique) ressemble à celui produit par un aimant droit placé au centre de la Terre :

Le champ magnétique terrestre est la résultante de deux composantes :

• $\overrightarrow{B_H}$ : composante horizontale du champ magnétique terrestre au point M.
• $\overrightarrow{B_V}$ : composante verticale du champ magnétique terrestre au point M.

L'axe géomagnétique, passant par les deux pôles magnétiques, fait un angle de $11,5°$ par rapport à l'axe de rotation de la Terre.

L'angle formé par $\overrightarrow{B_T}$ et $\overrightarrow{B_H}$ est appelé « inclinaison $\alpha$». Il augmente lorsque l'on se rapproche des pôles en tendant vers $90°$.

V- Exercices

5-1/ Exercice 1

En un point $M$ de l'espace, se superposent deux champs magnétiques $\overrightarrow{B_1}$ et $\overrightarrow{B_2}$ créés par deux aimants dont les directions sont orthogonales. Leurs intensités sont respectivement $B_1=5.{10}^{–3}T$ et $B_2=2.{10}^{–3}T$ :

1. Déterminer le pôle Nord de chaque aimant.

2. Représenter graphiquement le champ résultant $\overrightarrow{B}$.

3. Calculer l’intensité de $\overrightarrow{B}$ et $\alpha =\left(\overrightarrow{B},\overrightarrow{B_2}\right)$

V- Exercices

5-2/ Exercice 2

On considère deux aimants droits $A_1$ et $A_2$.

le pôle schématiser en noir est le pôle Nord.

L'aimant 1 crée au point $A$ un champ magnétique d'intensité $B_1=0,4T$.

L'aimant 2 crée au point $A$ un champ magnétique d'intensité $B_2=0,3T$.

1. Représenter pour chaque aimant, les vecteurs champs magnétiques $\overrightarrow{B_1}$ et $\overrightarrow{B_2}$ au point $A$ (Échelle : $1T\leftrightarrow 10cm$).

2. Déterminer graphiquement la résultante  du champ magnétique $\overrightarrow{B}$ au point $A$. Calculer son intensité $B$.

3. Dessiner l'orientation d'une boussole qu'on placerait au point $A$.

V- Exercices

5-3/ Exercice 3

On considère deux aimants droits $A_1$ et $A_2$ orientant les lignes de champ.

L'aimant 1 crée au point $A$ un champ magnétique d'intensité $B_1=2 mT$.

L'aimant 2 crée au point $A$ un champ magnétique d'intensité $B_2=3mT$.

1. Déterminer le pôle Nord de l’aimant $A_1$.

2. Représenter graphiquement $\overrightarrow{B_2}$ et le champ résultant $\overrightarrow{B}$.

3. Tracer et orienter les lignes de champ de l’aimant $A_2$ entre les deux pôles.

4. Quelle propriété possède le vecteur $\overrightarrow{B}$ dans cette région de l’espace champ magnétique ? Comment appelle-t-on un tel champ magnétique ?

V- Exercices

5-4/ Exercice 4

On considère deux aimants droits $A_1$ et $A_2$ créant chacun en $P$ des champs magnétiques notés respectivement $\overrightarrow{B_1}$ et $\overrightarrow{B_2}$. Leurs valeurs sont $B_1=30mT$ et $B_2=40mT$. Les axes des deux aimants sont perpendiculaires :

1. Compléter le schéma en indiquant les pôles des aimants.

2. Construire graphiquement en $P$ le champ magnétique $\overrightarrow{B}$ résultant de la superposition de $\overrightarrow{B_1}$ et $\overrightarrow{B_2}$.

3. Calculer la valeur $B$ de $\overrightarrow{B}$.

4. La valeur du champ magnétique terrestre $B_T$ est-elle négligeable devant $B$ ?

5. Calculer l’angle $\alpha$ entre la direction $D$ d’une aiguille aimantée placée en $P$ et l’axe $D_2$ de l’aimant $A_2$.

Donnée :

• La valeur du champ magnétique terrestre en $P$ est $B_T=47\mu T$.