Séance 9 - La dérivation d’une fonction numérique

Sommaire

I- La dérivabilité d’une fonction en un point

1-1/ Le nombre dérivé

1-2/ Interprétation géométrique du nombre dérivé – La tangente à la courbe en un point

1-3/ Approximation d’une fonction dérivable en un point par une fonction affine

II- Dérivabilité à droite - dérivabilité à gauche

2-1/ Définitions et propriétés

2-2/ Interprétation géométrique - Demi droite tangente en un point de la courbe

III- La fonction dérivé d’une fonction dérivable

3-1/ La fonction dérivé

3-2/ La fonction dérivée seconde - la fonction dérivée d’ordre n

3-3/ Fonction dérivée des fonctions usuelles

3-4/ Opérations sur les fonctions dérivables

IV- Applications de la dérivation

4-1/ Monotonie d’une fonction et signe de sa fonction dérivée

4-2/ Extremums d’une fonction dérivable

V- Équations différentielle $y"+w^{2}y=0$

VI- Exercices

6-1/ Exercice 1

6-2/ Exercice 2

6-3/ Exercice 3

6-4/ Exercice 4

6-5/ Exercice 5

6-6/ Exercice 6

I- La dérivabilité d’une fonction en un point

1-1/ Le nombre dérivé

Définition

Soit $f$ une fonction définie sur un intervalle ouvert $I$ et $a\in I$.

On dit que la fonction $f$ est dérivable en $a$, s’il existe un nombre réel $l$ tel que :

$\underset{h\to 0}{\lim }\frac{f\left(a+h\right)-f\left(a\right)}{h}=l$

Le réel $l$ est appelé le nombre dérivé de la fonction $f$ en $a$, il est noté : $f\text{'}\left(a\right)$

On écrit : $f\text{'}\left(a\right)=\underset{h\to 0}{\lim }\frac{f\left(a+h\right)-f\left(a\right)}{h}=l$ ou $f\text{'}\left(a\right)=\underset{x\to a}{\lim }\frac{f\left(x\right)-f\left(a\right)}{x-a}=l$

I- La dérivabilité d’une fonction en un point

1-1/ Le nombre dérivé

Exemple

Étudions la dérivabilité de la fonction $f:x\mapsto 2x^2$ en $a=1$

I- La dérivabilité d’une fonction en un point

1-2/ Interprétation géométrique du nombre dérivé – La tangente à la courbe en un point

I- La dérivabilité d’une fonction en un point

1-2/ Interprétation géométrique du nombre dérivé – La tangente à la courbe en un point

Définition

Soit $f$ une fonction dérivable en un point $a$ et $\left(C_f\right)$ sa courbe représentative dans un repère orthonormé $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$.

La droite $\left(T\right)$ qui passe par le point $A\left(a,f\left(a\right)\right)$ et qui est a pour coefficient directeur $f\text{'}\left(a\right)$ est appelée la tangente à la courbe $\left(C_f\right)$ au point $A$.

I- La dérivabilité d’une fonction en un point

1-2/ Interprétation géométrique du nombre dérivé – La tangente à la courbe en un point

Propriété

Soit $f$ une fonction dérivable en un point $a$.

Une équation de la droite tangente à la courbe $\left(C_f\right)$ de la fonction $f$ au point $A\left(a,f\left(a\right)\right)$ est :

$\left(T\right) : y=f\text{'}\left(a\right)\left(x-a\right)+f\left(a\right)$

I- La dérivabilité d’une fonction en un point

1-2/ Interprétation géométrique du nombre dérivé – La tangente à la courbe en un point

Exemple

Déterminons une équation de la tangente $\left(T\right)$ à la courbe de la fonction $x\mapsto f\left(x\right)=2x^2$ au point $A\left(1,f\left(1\right)\right)$.

I- La dérivabilité d’une fonction en un point

1-3/ Approximation d’une fonction dérivable en un point par une fonction affine

Définition

Soit $f$ une fonction dérivable en un point $a$.

La fonction $u:x\mapsto f\text{'}\left(a\right)\left(x-a\right)+f\left(a\right)$  est appelée la fonction affine tangente à la fonction $f$ au point $a$.

Le réel  $f\text{'}\left(a\right)\left(x-a\right)+f\left(a\right)$ est l’approximation affine du réel $f\left(x\right)$ au voisinage de $a$, on écrit :

$f\left(x\right)\underset{a}{~}f\text{'}\left(a\right)\left(x-a\right)+f\left(a\right)$

II- Dérivabilité à droite - dérivabilité à gauche

2-1/ Définitions et propriétés

Définition 1

Soit $f$ une fonction définie sur un intervalle de la forme : $\left([a;a+r[ r>0\right)$

On dit que $f$ est dérivable à droite en $a$ s’il existe un réel $l$ tel que : $\underset{h\to 0^{+}}{\lim }\frac{f\left(a+h\right)-f\left(a\right)}{h}=l$

Le réel $l$ est appelé le nombre dérivé de la fonction $f$ à droite en $a$, et on le note par : $f{\text{'}}_d\left(a\right)$

On écrit : $f{\text{'}}_d\left(a\right)=\underset{h\to 0^{+}}{\lim }\frac{f\left(a+h\right)-f\left(a\right)}{h}=\underset{x\to a^{+}}{\lim }\frac{f\left(x\right)-f\left(a\right)}{x-a}$

II- Dérivabilité à droite - dérivabilité à gauche

2-1/ Définitions et propriétés

Définition 2

Soit $f$ une fonction définie sur un intervalle de la forme : $\left(]a-r;a] r>0\right)$

On dit que $f$ est dérivable à gauche en $a$ s’il existe un réel $l$ tel que : $\underset{h\to 0^{-}}{\lim }\frac{f\left(a+h\right)-f\left(a\right)}{h}=l$

Le réel $l$ est appelé le nombre dérivé de la fonction $f$ à gauche en $a$, et on le note par : $f{\text{'}}_g\left(a\right)$

On écrit : $f{\text{'}}_g\left(a\right)=\underset{h\to 0^{-}}{\lim }\frac{f\left(a+h\right)-f\left(a\right)}{h}=\underset{x\to a^{-}}{\lim }\frac{f\left(x\right)-f\left(a\right)}{x-a}$

II- Dérivabilité à droite - dérivabilité à gauche

2-1/ Définitions et propriétés

Propriété

Soit $f$ une fonction définie sur un intervalle ouvert $I$ et $a\in I$.

$f$ est dérivable en $a$ si et seulement si $f$ est dérivable à droite en $a$ et $f$ est dérivable à gauche en $a$ et $f{\text{'}}_d\left(a\right)=f{\text{'}}_g\left(a\right)$

II- Dérivabilité à droite - dérivabilité à gauche

2-2/ Interprétation géométrique - Demi droite tangente en un point de la courbe

Si $f$ est dérivable à droite en , cela signifie graphiquement que la courbe de la fonction $f$ admet une demi-tangente au point $A\left(a;f\left(a\right)\right)$ d’équation : $\left(T_d\right) : y=f{\text{'}}_d\left(a\right)\left(x-a\right)+f\left(a\right)$

Si $f$ est dérivable à gauche en $a$, cela signifie graphiquement que la courbe de la fonction $f$ admet une demi-tangente au point $A\left(a;f\left(a\right)\right)$ d’équation : $\left(T_g\right) : y=f{\text{'}}_g\left(a\right)\left(x-a\right)+f\left(a\right)$

II- Dérivabilité à droite - dérivabilité à gauche

2-2/ Interprétation géométrique - Demi droite tangente en un point de la courbe

Résumé de La dérivabilité en un point - Interprétation géométrique du nombre dérivé

III- La fonction dérivé d’une fonction dérivable

3-1/ La fonction dérivé

Définitions

On dit qu’une fonction $f$ est dérivable sur un intervalle ouvert $]a;b[$ si $f$ est dérivable en tout point de $]a;b[$.

On dit qu’une fonction $f$ est dérivable sur l’intervalle fermer $[a;b]$ si $f$ est dérivable sur $]a;b[$ et $f$ dérivable à droite en $a$ et à gauche en $b$.

Si $f$ est dérivable sur un intervalle ouvert $I$, alors la fonction dérivée de $f$ est la fonction noté $f\text{'}$ est définie de $I$ vers $\mathrm{ℝ}$ :

$$\begin{gathered} f\text{'}:I\mapsto \mathrm{ℝ} \\ x\mapsto f\text{'}\left(x\right) \end{gathered}$$

III- La fonction dérivé d’une fonction dérivable

3-1/ La fonction dérivé

Exemples

1- Montrons la fonction $f$ définie sur $\mathrm{ℝ}$ par $f\left(x\right)=x^2$ est dérivable sur $\mathrm{ℝ}$ et déterminons la fonction dérivée $f\text{'}\left(x\right)$.

2- Etudier la dérivabilité de la fonction $g$ définie sur $[0;+\infty [$ par $g\left(x\right)=\sqrt{x}$ eet déterminons la fonction dérivée $g\text{'}\left(x\right)$  sur $0;+\infty [$.

III- La fonction dérivé d’une fonction dérivable

3-2/ La fonction dérivée seconde - la fonction dérivée d’ordre n

Définition

Soit $f$ est une fonction dérivable sur un intervalle $I$ de fonction dérivée $f\text{'}$.

Si $f\text{'}$ est aussi dérivable sur un intervalle $I$, alors on dit que $f$ est dérivable deux fois sur l’intervalle $I$ et la dérivée de $f\text{'}$ notés $f\text{'}\text{'}$ est appelée la dérivée seconde de la fonction $f$, et on a : $f\text{'}\text{'}=\left(f\text{'}\right)\text{'}$

Si $f$ est $n$ fois sur l’intervalle $I$ $\left(n\in \mathrm{\mathbb{N}}*\right)$, alors la fonction dérivée de $f$ d’ordre $n$ noté $f^{\left(n\right)}$ :

$$\begin{gathered} f^{\left(n\right)}:I\mapsto \mathrm{ℝ} \\ x\mapsto f^{\left(n\right)}\left(x\right) \end{gathered}$$

III- La fonction dérivé d’une fonction dérivable

3-2/ La fonction dérivée seconde - la fonction dérivée d’ordre n

Exemple

Montrons que la fonction $f$ définie par $f\left(x\right)=x^2$ est dérivable deux fois sur $\mathrm{ℝ}$ et déterminons $f\text{'}\text{'}\left(x\right)$.

III- La fonction dérivé d’une fonction dérivable

3-3/ Fonction dérivée des fonctions usuelles

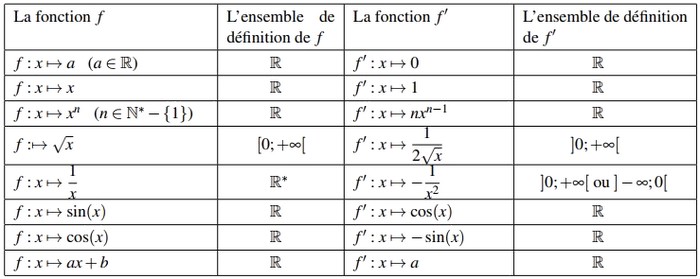
III- La fonction dérivé d’une fonction dérivable

3-4/ Opérations sur les fonctions dérivables

Propriété

Si $f$ et $g$ sont deux fonction dérivables sur un intervalle $I$ et $k\in \mathrm{ℝ}$, alors on a :

1) La fonction $f+g$ est dérivable sur l’intervalle $I$ et on a : $\left(f+g\right)\text{'}=f\text{'}+g\text{'}$

2) La fonction $k.f$ est dérivable sur l’intervalle $I$ et on a : $\left(k.f\right)\text{'}=k.f\text{'}$

3) La fonction $f\times g$ est dérivable sur l’intervalle $I$ et on a : $\left(f\times g\right)\text{'}=f\text{'}\times g+f\times g\text{'}$

4) Si de plus $\left(\forall x\in I\right) g\left(x\right)\ne 0$, alors :

• La fonction $\frac{1}{g}$ est dérivable sur l’intervalle $I$ et on a : ${\left(\frac{1}{g}\right)}^{\text{'}}=\frac{-g\text{'}}{g^2}$
• La fonction $\frac{f}{g}$ est dérivable sur l’intervalle $I$ et on a : ${\left(\frac{f}{g}\right)}^{\text{'}}=\frac{f\text{'}\times g-f\times g\text{'}}{g^2}$

III- La fonction dérivé d’une fonction dérivable

3-4/ Opérations sur les fonctions dérivables

Remarque

Toute fonction polynôme est dérivable sur $\mathrm{ℝ}$.

Toute fonction rationnelle est dérivable sur chaque intervalle inclus dans son ensemble de définition.

III- La fonction dérivé d’une fonction dérivable

3-4/ Opérations sur les fonctions dérivables

Propriété

Si $f$ est une fonction dérivable et strictement positive sur un intervalle $I$, alors la fonction $\sqrt{f}$ est dérivable sur $I$ et :

$\left(\sqrt{f}\right)\text{'}=\frac{f\text{'}}{2\sqrt{f}}$

IV- Applications de la dérivation

4-1/ Monotonie d’une fonction et signe de sa fonction dérivée

Propriété

Soit $f$ une fonction dérivable sur un intervalle $I$.

- Si $f$ est croissante sur l’intervalle $I$, alors : $\left(\forall x\in I\right) f\text{'}\left(x\right)\ge 0$

- Si $f$ est décroissante sur l’intervalle $I$, alors : $\left(\forall x\in I\right) f\text{'}\left(x\right)\le 0$

- Si $f$ est constante sur l’intervalle $I$, alors : $\left(\forall x\in I\right) f\text{'}\left(x\right)=0$

IV- Applications de la dérivation

4-1/ Monotonie d’une fonction et signe de sa fonction dérivée

Propriété

Soit $f$ une fonction dérivable sur un intervalle $I$.

- Si la dérivée $f\text{'}$ est strictement positive sur l’intervalle $I$, sauf peut-être en des points isolés de $I$ où $f\text{'}$ s’annule, alors la fonction $f$ est strictement croissante sur $I$

- Si la dérivée $f\text{'}$ est strictement négative sur l’intervalle $I$, sauf peut-être en des points isolés de $I$ où $f\text{'}$ s’annule, alors la fonction $f$ est strictement décroissante sur $I$.

- Si $f\text{'}$ est nulle sur $I$, alors $f$ est constante sur $I$.

IV- Applications de la dérivation

4-2/ Extremums d’une fonction dérivable

Propriété

Soit $f$ une fonction dérivable sur un intervalle ouvert $I$ et $a\in I$.

Si $f$ admet un extremum local au point $a$, alors $f\text{'}\left(a\right)=0$.

V- Équations différentielle $y"+w^{2}y=0$

Définition

Soit $w$ un nombre réel non nul.

L’équation $y"+w^{2}y=0$ où l’inconnue est une fonction $y$ telle que $y"$ est sa dérivée seconde est appelée équation différentielle.

Toute fonction $f$ deux fois dérivable sur $\mathrm{ℝ}$ et vérifie l’égalité $f"\left(x\right)+w^{2}f\left(x\right)=0$, pour tout $x\in \mathrm{ℝ}$ est appelée solution de l’équation différentielle $y"+w^{2}y=0$.

V- Équations différentielle $y"+w^{2}y=0$

Propriété

Soit $w$ un nombre réel non nul.

La solution générale de l’équation différentielle $y"+w^{2}y=0$ est l’ensemble des fonctions $y$ définies sur $\mathrm{ℝ}$ par $x\mapsto y\left(x\right)=\alpha \cos \left(wx\right)+\beta \sin \left(wx\right)$ où $\alpha ,\beta \in \mathrm{ℝ}$

VI- Exercices

6-1/ Exercice 1

1. Étudier la dérivabilité de la fonction $f$ au point $x_0$, puis donner une interprétation géométrique du résultat obtenu dans chacun des cas suivants :

VI- Exercices

6-2/ Exercice 2

Soit la fonction $f$ définie par :

$\left\{\begin{array}{c}f\left(x\right)=2x^2-3x-1 si x<1\\ f\left(x\right)=\frac{x-3}{2x-1} si x>1 \\ f\left(1\right)=-2 \end{array}\right.$

1. Étudier la dérivabilité de $f$ à droite en $1$, et donner une interprétation géométrique du résultat.

2. Étudier la dérivabilité de $f$ à gauche en $1$, et donner une interprétation géométrique du résultat.

3. Étudier la dérivabilité de $f$ au point $1$.

VI- Exercices

6-3/ Exercice 3

Soit la fonction $f$ définie par :

$\left\{\begin{array}{c}f\left(x\right)=x^3+2x^2+x+3 si x<-1\\ f\left(x\right)=\frac{x+4}{2x+3} si x>-1 \\ f\left(-1\right)=3 \end{array}\right.$

1. Étudier la dérivabilité de $f$ à droite en $-1$, et donner une interprétation géométrique du résultat.

2. Étudier la dérivabilité de $f$ à gauche en $-1$, et donner une interprétation géométrique du résultat.

3. Étudier la dérivabilité de $f$ au point $-1$.

VI- Exercices

6-4/ Exercice 4

1. Déterminer la fonction dérivée de la fonction $f$ dans chacun des cas suivants :

VI- Exercices

6-5/ Exercice 5

Soit $f$ la fonction suivante : $f\left(x\right)={\left(\frac{3x-2}{2x+3}\right)}^4$

1. Déterminer $D_f$ le domaine de définition de $f$.

2. Étudier la dérivabilité de $f$ sur $D_f$.

3. Déterminer l’équation cartésienne de la droite tangente $\left(T\right)$ à la courbe de $f$ au point $A(\frac{2}{3};0)$.

4. Déterminer $f\text{'}\left(x\right)$ la dérivée de $f$ sur $D_f$.

VI- Exercices

6-6/ Exercice 6

Partie 1

On considère la fonction $g$ définie sur $I=[-2;3]$ par $g\left(x\right)=3x-x^3$.

1. Calculer $g\text{'}\left(x\right)$ la fonction dérivée de $g$ sur $I$.

2. Étudier les variations de $g$, puis donner son tableau de variations sur $I$.

3. Déterminer les extremum de $g$ sur $]-\frac{3}{2};0[$ et $\left[-2;0\right]$ et $I$.

Partie 2

1. Résoudre dans $\mathrm{ℝ}$ les équations différentielles suivantes :

$$\begin{gathered} \overline{)1} y"+3y=0 \\ \overline{)2} y"+2y=0 \\ \overline{)3} 6y"+3y=0 \end{gathered}$$