
Physique et Chimie : 2ème Année Bac
Séance 27 (Atome et mécanique de Newton)
Professeur : Mr El GOUFIFA Jihad
Sommaire
I- Les limites de la mécanique newtonienne
1-1/ Analogie entre l’interaction gravitationnelle et électrostatique
1-2/ Modèle planétaire de l’atome
1-3/ Limites de la mécanique classique
II- Quantification des échanges d'énergie
2-1/ Les photons
2-2/ Relation de Planck-Einstein
2-3/ Les postulats de Bohr (Modèle de Bohr de l'atome)
III- Quantification d’énergie des atomes
3-1/ Niveaux d’énergie des atomes
3-2/ Diagramme énergétique des atomes
IV- Spectre d'émission et spectre d'absorption
4-1/ Spectre d'émission de l'atome d'hydrogène
4-2/ Séries de spectre d'émission de l'atome d'hydrogène
V- Exercices
5-1/ Exercice 1
5-2/ Exercice 2
5-3/ Exercice 3
5-4/ Exercice 4
I- Les limites de la mécanique newtonienne
1-1/ Analogie entre l’interaction gravitationnelle et électrostatique
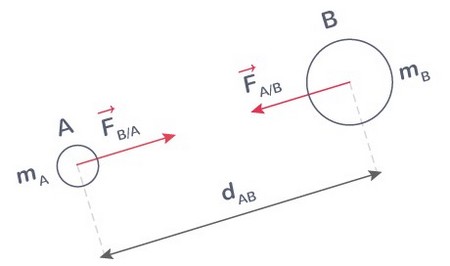
Interactions gravitationnelles (Loi de Newton)
Deux corps A et B de masses et exercent l'un sur l'autre des forces d'attraction gravitationnelle de même intensité :
Interactions électrostatiques (Loi de Coulomb)
Deux corps (A) et (B) ponctuelles, de charges respectives et , séparés par une distance d, exercent l’un sur l’autre une force d’attraction, donnée par :
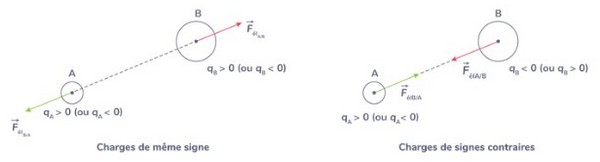
Analogie entre les forces gravitationnelle et électrique
- Leur droite d’action joint les corps en interaction.
- Leur valeur est proportionnelle à , représentant la distance séparant les deux corps en interaction.
- Elles sont dites forces newtoniennes.

I- Les limites de la mécanique newtonienne
1-2/ Modèle planétaire de l’atome
Après l’expérience fameuse de Rutherford (expérience de la feuille d’or), il prouve que l’atome est constituée du vide, donc Rutherford utilise l’analogie entre l’interaction gravitationnelle macroscopique, et celle électrostatique microscopique, et propose un modèle planétaire de l’atome, basée sur la mécanique classique :
L’atome est constituée d’un noyau autour duquel les électrons tournent.
Exemple
L’atome d’hydrogène : Un noyau correspond à la terre, autour de laquelle un satellite (l’électron) tourne.

I- Les limites de la mécanique newtonienne
1-3/ Limites de la mécanique classique
Ce modèle porte plusieurs contradictions :
- Les rayons orbitaux possibles : L’orbite de l’électron peut être loin du noyau à n’importe quel rayon, ce qui résulte plusieurs volumes possible d’une atome.
- L’effet photoélectrique : L’émission d’électrons par un métal, lorsqu’il est soumis à une onde électromagnétique.
- La discontinuité du spectre d’émission...
Ceci prouve que la mécanique de Newton est inutile au niveau microscopique.
II- Quantification des échanges d'énergie
2-1/ Les photons
En 1900, Max PLANCK émet l’hypothèse que la lumière, comme toutes les ondes électromagnétiques, transporte de l’énergie par « paquets », appelés quanta d’énergie.
Il postule alors la quantification de l’énergie transportée par les ondes électromagnétiques.
En 1905, Albert EINSTEIN émet l’hypothèse que ces quanta d’énergie sont portés par des particules appelées photons.
Les photons sont des corpuscules de masse nulle, non chargées, se propageant à la vitesse de la lumière, , dans le vide.
II- Quantification des échanges d'énergie
2-2/ Relation de Planck-Einstein
Chaque onde électromagnétique caractérisée par une fréquence et une longueur d’onde est constitué de photons (grains élémentaires), et chaque photon a pour énergie :
- : constante de Planck :
- : fréquence de la lumière :
- : célérité de la lumière dans le vide.
- : longueur d’onde
II- Quantification des échanges d'énergie
2-3/ Les postulats de Bohr (Modèle de Bohr de l'atome)
Les variations d’énergie d’un atome sont quantifiées.
L’atome ne peut exister que dans certains états d’énergies bien définis, caractérisés par un niveau d’énergie.
Un photon de fréquence ν est émis lorsque l’atome effectue une transition entre deux niveaux d’énergies et , tel que :

III- Quantification d’énergie des atomes
3-1/ Niveaux d’énergie des atomes
L'atome peut passer d'un état à un autre état en gagnant ou en perdant de l'énergie.
Pour expliquer cet échange d'énergie entre l'atome et le milieu extérieure, Bohr a supposé que l'énergie de l'atome est quantifiée et il a proposé la relation qui permet de déterminer les différents niveaux de l'atome d'hydrogène.
Dans cette relation le nombre quantique principal « n » est un nombre entier non nul et .
- Si , c’est le niveau d’énergie minimal, autrement c’est le niveau stable et fondamental de l’atome.
- Si , l’atome est dans un état excité, l’énergie devient supérieur en fonction de n, c-à-d : .
- Si , alors , l’atome est dans un état dit ionisé, (pas d’électron).
III- Quantification d’énergie des atomes
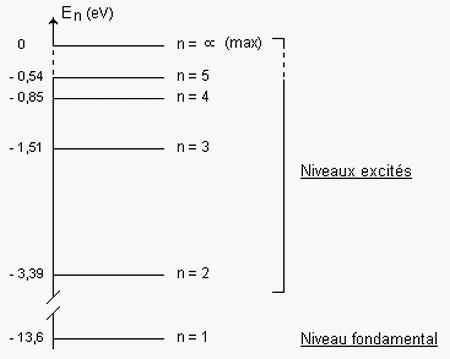
3-2/ Diagramme énergétique des atomes
Diagramme énergétique de l'atome d'hydrogène
IV- Spectre d'émission et spectre d'absorption
4-1/ Spectre d'émission de l'atome d'hydrogène
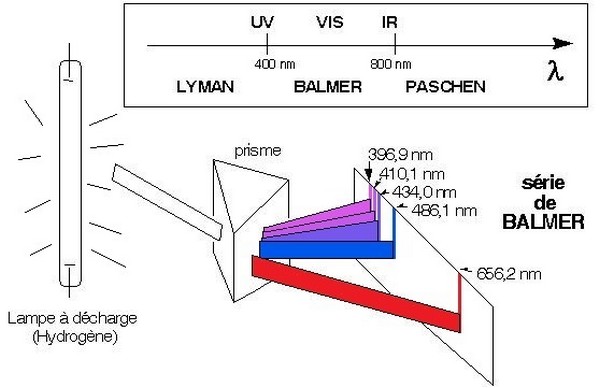
Expérience de Balmer
Par décharge électrique dans une ampoule contenant le gaz dihydrogène on obtient le spectre d'émission de l'atome d'hydrogène, c'est un spectre de raies discontinu, il contient quatre raies visibles et d'autres raies invisibles :
IV- Spectre d'émission et spectre d'absorption
4-1/ Spectre d'émission de l'atome d'hydrogène
Interprétation
Par excitation avec la décharge électrique l'électron de chaque atome d'hydrogène passe à un niveau d'énergie plus élevé (les atomes sont dits excités) par la suite ces électrons perdent leurs excitations en passant à un niveau d'énergie plus bas.
Cette transition entraîne l'émission de radiations de longueurs d'ondes bien déterminées et on obtient le spectre d'émission.
La relation qui correspond au passage de l'atome excité d'un niveau d'énergie à un niveau d'énergie inférieure est :
: Conctante de Rydberg
Donc la longueur d'onde liée à la radiation émise est :
IV- Spectre d'émission et spectre d'absorption
4-2/ Séries de spectre d'émission de l'atome d'hydrogène
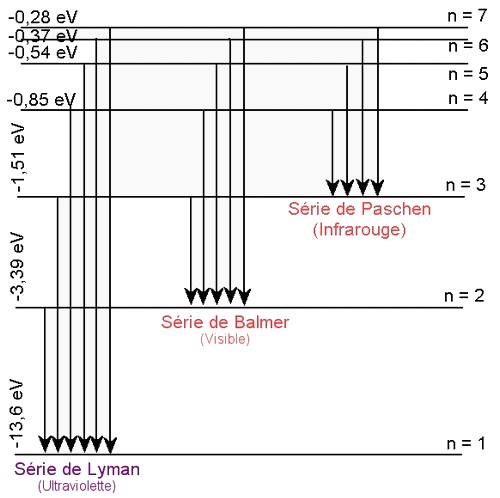
On voit que le spectre d'émission (ou d'absorption) de l'hydrogène présente de nombreuses raies groupées par séries.
Lorsque la transition électronique aboutit sur le niveau fondamental (n=1), c'est la série de Lyman, elle se trouve dans le domaine U.V.
Lorsque la transition électronique aboutit sur le premier niveau excité (n=2), c'est la série de Balmer, elle se trouve en grande partie dans le domaine visible.
Lorsque la transition électronique aboutit sur le deuxième niveau excité (n=3), c'est la série de Paschen, elle se trouve dans le domaine I.R.
V- Exercices
5-1/ Exercice 1
- Déterminer les longueurs d’onde émises par la désexcitation de l’atome dont le diagramme énergétique est sur la figure suivante sachant que son énergie initiale est .

- Préciser le domaine auquel appartient chaque rayonnement.
On suppose, cette fois, que l’énergie de l’atome ne peut excéder .
- Quelles doivent être les longueurs d’onde de photons incidents pour que l’atome puisse les absorber ?
V- Exercices
5-2/ Exercice 2
L’énergie d’un atome d’hydrogène au niveau est , avec pour .
- Comment s’appelle le niveau ? les niveaux correspondant à ?
On considère que varie de 1 à 8 (valeurs entières) ou que .
- Expliquer succinctement pourquoi ce dernier état correspond à l’ionisation.
- Calculer la longueur d’onde minimale d’un photon permettant d’ioniser l’atome d’hydrogène initialement dans son état (énergie de première ionisation).
- Refaire le même calcul pour .
Un photon, de longueur d’onde , est absorbé par un atome d’hydrogène dans son état le plus stable.
- Calculer la vitesse de l'électron éjecté (en supposant que le noyau reste immobile).
- Exprimer l’énergie de première ionisation d’un hydrogénoïde (atome ou ion à un seul électron, soit , , , ...) en fonction de et sachant que l’énergie d’un hydrogénoïde au niveau n est , où est le numéro atomique. Conclure.
Données :
- .
V- Exercices
5-3/ Exercice 3
Les groupements caractéristiques de la chimie organique absorbent des radiations électromagnétiques qui permettent d’identifier les molécules. Ces absorptions se présentent sous la forme des bandes d’absorption qui sont caractérisées par leur nombre d’onde moyen en .
Le tableau suivant rassemble quelques valeurs typiques :
| Groupement caractéristiques | |||
| 1700 | 3350 | 1650 |
- Calculer en les énergies des radiations absorbées par ces groupements caractéristiques.
- Que peut-on déduire de l’existence de bandes d’absorption quand à l’énergie d’une molécule ?
On considère deux molécules le butan-2-one et le butan-2-ol.
- Écrire la formule semi-développée de chaque molécule.
- Attribuer à chacun des spectres suivant la molécule correspondante.

V- Exercices
5-4/ Exercice 4
Le bismuth 212, , radioactive de type . Il se désintègre en thallium 208.
Le diagramme énergétique suivant représente le niveau d’énergie du noyau père, de bismuth, et ceux du noyau fils :
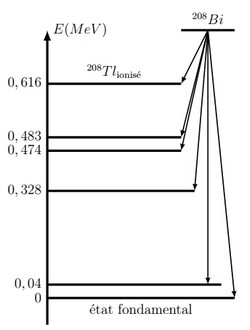
- Quel niveau est choisi pour référence de l’énergie ?
- Écrire l’équation de la désintégration .
- Calculer la plus grande longueur d’onde des rayons émis lors de la désexcitation du noyau fils.
- Faire de même pour la plus courte longueur d’onde.


