
Physique et Chimie : 2ème Année Bac
Séance 26B (Aspects énergétiques – Pendule pesant et de torsion)
Professeur : Mr EL GOUFIFA Jihad
Sommaire
I- Pendule de torsion
1-1/ Énergie cinétique
1-2/ Énergie potentielle de torsion
1-3/ Énergie mécanique
1-4/ Diagramme énergétique
II- Pendule pesant
2-1/ Énergie cinétique
2-2/ Énergie potentielle de pesanteur
2-3/ Énergie mécanique
2-4/ Diagramme énergétique
III- Exercices
3-1/ Exercice 1
3-2/ Exercice 2
3-3/ Exercice 3
I- Pendule de torsion
1-1/ Énergie cinétique
On considère un pendule de torsion formé d’un fil métallique léger auquel est fixé une tige dense.
Soit le moment d’inertie de la tige par rapport à l’axe de rotation matérialisé par le fil métallique et est la vitesse angulaire de la tige à instant .
On définit l’énergie cinétique du système qu’est en rotation autour de , à cet instant par l’expression suivante :
I- Pendule de torsion
1-2/ Énergie potentielle de torsion
L’énergie potentielle de torsion d’un pendule de torsion est définie par la relation :
Avec la constante de la torsion du pendule, angle de torsion en rad et une constante qui dépend du choix de l’état de référence fourni par les conditions initiales.
En générale , on prend pour ; soit d’où
I- Pendule de torsion
1-3/ Énergie mécanique
On a :
Les oscillations sont non-amorties, donc on a un échange entre l’énergie potentielle et cinétique, alors que celle mécanique reste constante.
On dérive par rapport au temps :
C’est la même équation différentielle obtenue à partir de l’étude dynamique.
I- Pendule de torsion
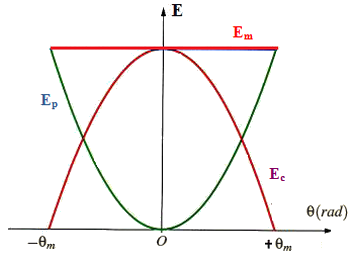
1-4/ Diagramme énergétique
Les frottements sont négligeables, donc on a une conservation d’énergie mécanique :
Lorsque la tige passe par sa position d’équilibre : et , soit et
Lorsque la tige passe par ses positions extrêmes : et , soit et
II- Pendule pesant
2-1/ Énergie cinétique
L'énergie cinétique du pendule pesant est :
II- Pendule pesant
2-2/ Énergie potentielle de pesanteur
L'énergie potentielle de pesanteur du pendule pesant est :
En considérant comme état de référence lorsque , la constante et donc:
Lorsque le pendule pesant est incliné d'un angle , son énergie potentielle de pesanteur est :
II- Pendule pesant
2-3/ Énergie mécanique
On a :
Les oscillations sont non-amorties, donc on a un échange entre l’énergie potentielle et cinétique, alors que celle mécanique reste constante.
On dérive par rapport au temps :
C’est la même équation différentielle obtenue à partir de l’étude dynamique.
II- Pendule pesant
2-4/ Diagramme énergétique
Les frottements sont négligeables, donc on a une conservation d’énergie mécanique :

Pour les petites oscillations , on a
Donc on peut écrire par approximation :
Et on obtient le diagramme suivant :

III- Exercices
3-1/ Exercice 1
Une tige homogène de masse et de longueur pouvant tourner dans un plan vertical autour d’un axe horizontal fixe passant par son extrémité A.
Le moment d’inertie de cette tige par rapport à l’axe est .
On repère à chaque instant la position du pendule pesant par l’abscisse angulaire orienté :
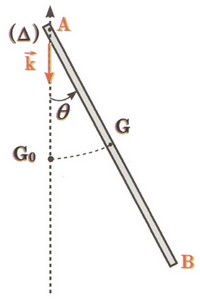
On choisit le plan horizontal contenant le point position du centre d’inertie de la tige à l’équilibre comme état de référence de l’énergie potentielle de pesanteur .
On admet dans le cas de faible amplitude que , et on prend .
- Montrer que l’expression de l’énergie potentielle de pesanteur du pendule pesant peut s’écrire sous la forme : .
- Dans le cas de faible amplitude, écrire l’expression de l’énergie mécanique à un instant en fonction de , , , et .
- En déduire l’équation différentielle vérifiée par l’abscisse angulaire dans le cas de faible amplitude.
On lance la tige à partir de sa position d’équilibre avec une vitesse initiale. Elle acquiert dans chaque cas une énergie mécanique donnée :
- dans le cas 1 :
- dans le cas 2 :
Le diagramme suivant donne l’évolution de l’énergie potentielle et de l’énergie mécanique du pendule pesant dans chaque cas :

- Déterminer à l’aide du diagramme, la nature du mouvement du pendule dans chaque cas.
- Préciser à partir du diagramme, la valeur maximale de l’abscisse angulaire du pendule dans le cas 1. En déduire la masse de la tige.
Dans le deuxième cas, l’énergie cinétique du pendule pesant varie entre une valeur minimale et une valeur maximale .
- Trouver les valeurs de et .
III- Exercices
3-2/ Exercice 2
On considère un pendule de torsion constitué d’un fil de torsion et d’une barre homogène de moment d’inertie .
On écarte la barre de sa position d’équilibre d’un angle par rapport à la position d’équilibre , et on la libère sans vitesse initiale à l’instant :

Les amortissements sont négligeables.
- Montrer que le mouvement de la barre est un mouvement oscillatoire sinusoïdale.
- Montrer que où désigne la période propre du mouvement du pendule.
- Sachant que , et la constante de torsion , calculer l’énergie cinétique maximale du pendule de torsion.
III- Exercices
3-3/ Exercice 3
On étudie le mouvement d’un pendule de torsion dans un repère lié à un référentiel terrestre supposé galiléen.
On repère la position de la tige MN à chaque instant par l’abscisse angulaire orientée comme l’indique la figure suivante :

On prend pour état de référence de l’énergie potentielle de torsion pour , et on prend .
Le pendule effectue des oscillations d’amplitude . L’étude expérimentale a permis d’obtenir la courbe suivante :
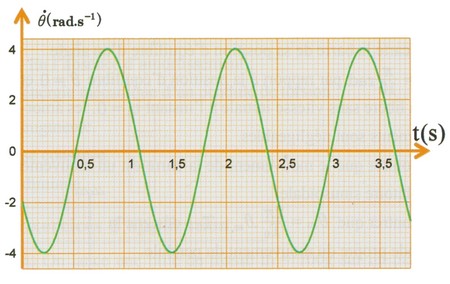
- En appliquant la relation fondamentale de la dynamique dans le cas de la rotation, établir l’équation différentielle du mouvement du pendule.
La solution de cette équation différentielle s’écrit sous la forme où est la période propre du pendule.
- Montrer que l’expression numérique de la vitesse angulaire s’écrit sous la forme .
- Déterminer la valeur de la constante de torsion .
- Déterminer la valeur de l’énergie mécanique de l’oscillateur et en déduire la valeur de son énergie potentielle à l’origine des dates .


