Séance 16 - Parallélogramme

Sommaire

I- Le parallélogramme

1-1/ Définition

1-2/ Exemple

II- Propriétés

2-1/ Propriété des diagonales

2-2/ Propriété des côtés opposés

2-3/ Propriété des angles opposés

2-4/ Propriété des angles consécutifs

III- Exercices

3-1/ Exercice 1

3-2/ Exercice 2

3-3/ Exercice 3

3-4/ Exercice 4

3-5/ Exercice 5

3-6/ Exercice 6

3-7/ Exercice 7

I- Le parallélogramme

1-1/ Définition

Le parallélogramme est un quadrilatère dont les supports des côtés opposés sont parallèles.

I- Le parallélogramme

1-2/ Exemple

Soit ABCD un parallélogramme.

II- Propriétés

2-1/ Propriété des diagonales

Propriété directe

Dans un parallélogramme les diagonales se coupent en leur milieu, appelé centre du parallélogramme.

Exemple

Soit ABCD un parallélogramme de centre O.

II- Propriétés

2-1/ Propriété des diagonales

Propriété réciproque

Si dans un quadrilatère les diagonales se coupent en leur milieu, alors c’est un parallélogramme.

Exemple

II- Propriétés

2-2/ Propriété des côtés opposés

Propriété directe

Dans un parallélogramme, les côtés opposés sont isométriques (égaux).

Exemple

Soit ABCD un parallélogramme.

On a : AB=DC et AD=BC

II- Propriétés

2-2/ Propriété des côtés opposés

Propriété réciproque

Si dans un quadrilatère les côtés opposés sont isométriques (égaux), alors c’est un parallélogramme.

Exemple

II- Propriétés

2-2/ Propriété des côtés opposés

Propriété réciproque (particulière)

Si dans un quadrilatère, deux côtés opposés sont isométriques (égaux) et leurs supports sont parallèles, alors c’est un parallélogramme.

Exemple

II- Propriétés

2-3/ Propriété des angles opposés

Propriété directe

Dans un parallélogramme, les angles opposés sont isométriques (égaux).

Exemple

Soit ABCD un parallélogramme.

On a : $\widehat{ABC}=\widehat{ADC}$ et $\widehat{DAB}=\widehat{DCB}$

II- Propriétés

2-3/ Propriété des angles opposés

Propriété réciproque

Si dans un quadrilatère les angles opposés sont isométriques (égaux), alors c’est un parallélogramme.

Exemple

II- Propriétés

2-4/ Propriété des angles consécutifs

Propriété directe

Dans un parallélogramme les angles consécutifs sont supplémentaires (la somme de leurs mesures égale à 180°).

Exemple

Soit ABCD un parallélogramme.

On a : 

$$\begin{gathered} \widehat{ABC}+\widehat{BCD}=180° \\ \widehat{BCD}+\widehat{CDA}=180° \\ \widehat{CDA}+\widehat{DAB}=180° \\ \widehat{DAB}+\widehat{ABC}=180° \end{gathered}$$

III- Exercices

3-1/ Exercice 1

Pour chaque énoncé, complète les données, la propriété et la conclusion :

III- Exercices

3-2/ Exercice 2

Pour chaque énoncé, complète les données, la propriété et la conclusion :

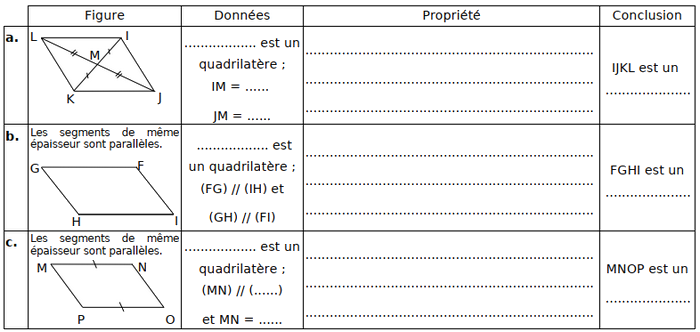
III- Exercices

3-3/ Exercice 3

Complète les démonstrations suivantes :

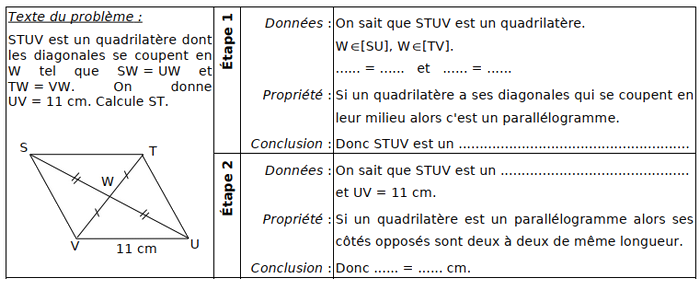
III- Exercices

3-4/ Exercice 4

Dans la figure suivante, on a :

$\left(EF\right)\parallel \left(AN\right) ; \left(MN\right)\parallel \left(FG\right) ; \left(MB\right)\parallel \left(EG\right)$

• Montrer que : $FA=BG$.

III- Exercices

3-5/ Exercice 5

On considère la figure suivante où $ABCD$ et $BEFC$ sont deux parallélogrammes.

1. Donnez, en justifiant, deux droites parallèles à la droite $\left(BC\right)$.

2. Démontrez que $AEFD$ est un parallélogramme.

3. Démontrez que les segments $\left[AF\right]$ et $\left[ED\right]$ se coupent en leur milieu.

III- Exercices

3-6/ Exercice 6

$EFGH$ est un parallélogramme de centre $I$.

$A$ est un point de $\left[HF\right]$.

1. Construire $B$ le symétrique de $A$ par rapport à $I$.

2. Montrer que le quadrilatère $AEBG$ est un parallélogramme.

III- Exercices

3-7/ Exercice 7

$ABCD$ et $BEDF$ sont deux parallélogrammes.

Soit $O$ le centre de $BEDF$.

1. Montrer que $O$ est le milieu de $\left[AC\right]$.

2. Montrer que $AECF$ est un parallélogramme.