
Mathématiques : 2Bac SPC-SVT-Agro-STE-STM
Séance 14 (Géométrie dans l’espace 1 : Produit scalaire)
Professeur : Mr CHEDDADI Haitam
Sommaire
I- Produit scalaire dans l’espace
1-1/ Définition
1-2/ Remarques
1-3/ Propriétés
II- Base et repère orthonormé
2-1/ Rappel
2-2/ Technique
2-3/ Définitions
III- Expression analytique de
IV- Ensemble des points tel que
V- Plan déterminé par un point et un vecteur normal
5-1/ Vecteur normal à un plan
5-2/ Ensemble des points tel que
5-3/ Ensemble des points tel que
VI- Distance d’un point à un plan
6-1/ Définition
6-2/ Propriété
VII- Parallélisme et orthogonalité des droites et des plans
7-1/ Parallélisme et orthogonalité de deux plans
7-2/ Parallélisme et orthogonalité d’une droite et un plan
IIX- Étude analytique de la sphère
8-1/ Définition d'une sphère
8-2/ Équation cartésienne d’une sphère
8-3/ Équation cartésienne d’une sphère déterminée par un diamètre
8-4/ L’ensemble des points tel que
8-5/ Positions relatives d’une sphère et un plan
8-6/ Positions relatives d’une sphère et une droite
IX- Exercices
9-1/ Exercice 1
9-2/ Exercice 2
9-3/ Exercice 3
9-4/ Exercice 4
9-5/ Exercice 5
9-6/ Exercice 6
I- Produit scalaire dans l’espace
1-1/ Définition
Soient et deux vecteurs non nul de l’espace
, et sont trois points de tel que et
est la projection de sur la droite .
Le produit scalaire de et est noté par ou tel que :
Cas 1
Cas 2
I- Produit scalaire dans l’espace
1-2/ Remarques
est le carré scalaire de et est toujours positif.
est la norme du vecteur , on note : .
.
et sont colinéaire
Exemple
I- Produit scalaire dans l’espace
1-3/ Propriétés
et et trois vecteurs de l’espace et .
On a :
Symétrie du produit scalaire :
Positivité du produit scalaire :
Non dégénère :
Linéarité du produit scalaire :
Exemple
I- Base et repère orthonormé
2-1/ Rappel
et et trois vecteurs de l’espace rapporté à une base
Le déterminant des vecteurs et et dans cet ordre est le nombre :
et et sont coplanaires si et seulement si
I- Base et repère orthonormé
2-2/ Technique
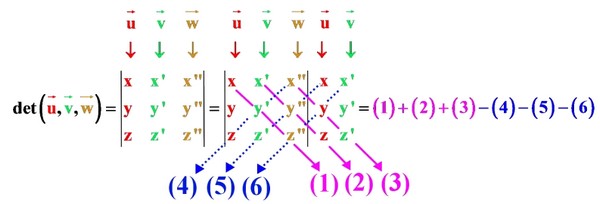
Exemple
I- Base et repère orthonormé
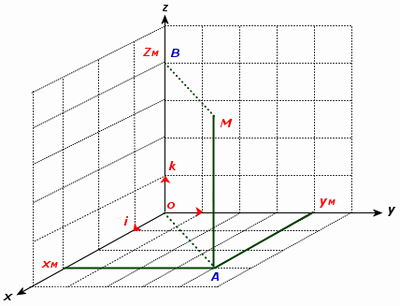
2-3/ Définitions
est une base de l’espace équivaut à et et ne sont pas coplanaires :
Prenons un point de l’espace
Le quadruplé est appelé repère de
Si et , alors :
- La base est une base orthonormée.
- Le repère est un repère orthonormé.
Exemple
III- Expression analytique de
Propriété
Le produit scalaire de et est :
La norme du vecteur est : .
La distance est : .
Exemple
IV- Ensemble des points tel que
Propriété
est un point et est un vecteur non nul de l’espace et .
L’ensemble des points de l’espace tel que est un plan d’équation de la forme :.
Exemple
V- Plan déterminé par un point et un vecteur normal
5-1/ Vecteur normal à un plan
Définition
Tout vecteur non nul sa direction est perpendiculaire au plan s’appelle vecteur normal au plan .
Remarques
Si est normale au plan , alors et .
Si est normale au plan et passe par le plan est noté par .
Exemple
V- Plan déterminé par un point et un vecteur normal
5-1/ Vecteur normal à un plan
Définition
Tout vecteur non nul sa direction est perpendiculaire au plan s’appelle vecteur normal au plan .
Remarques
Si est normale au plan , alors et .
Si est normale au plan et passe par le plan est noté par .
Exemple
V- Plan déterminé par un point et un vecteur normal
5-2/ Ensemble des points tel que
Propriété
L’ensemble des points de l’espace qui vérifie avec est un plan, et le vecteur non nul est un vecteur normal à ce plan.
Exemple
V- Plan déterminé par un point et un vecteur normal
5-3/ Ensemble des points tel que
Propriété 1
est un vecteur non nul et est un point de l’espace .
L’ensemble des points de l’espace qui vérifie est le plan qui passe par et le vecteur est un vecteur normal à ce plan (c.à.d. ).
Le plan a une équation cartésienne de la forme avec .
Exemple
V- Plan déterminé par un point et un vecteur normal
5-3/ Ensemble des points tel que
Propriété 2
Tout plan a pour équation cartésienne de la forme la réciproque avec .
Exemple
VI- Distance d’un point à un plan
6-1/ Définition
est un plan et est un point de l’espace et est la projection orthogonale de sur le plan .
La distance du point au plan est , et on note .
Exemple
VI- Distance d’un point à un plan
6-2/ Propriété
est un plan et est un point de l’espace tel que a pour équation .
La distance du point au plan est :
Exemple
VII- Parallélisme et orthogonalité des droites et des plans
7-1/ Parallélisme et orthogonalité de deux plans
Propriété
Soient et .
 |
|
 |
Exemple
VII- Parallélisme et orthogonalité des droites et des plans
7-1/ Parallélisme et orthogonalité de deux plans
Propriété
Soient et
 |
|
 |
Exemple
IIX- Étude analytique du sphère
8-1/ Définition d'une sphère
est un point donné de l’espace et
L’ensemble des points de l’espace tel que s’appelle le sphère de centre et de rayon .
On note ou
IIX- Étude analytique du sphère
8-2/ Équation cartésienne d’une sphère
L'équation cartésienne de est :
avec
IIX- Étude analytique du sphère
8-3/ Équation cartésienne d’une sphère déterminée par un diamètre
Définition
est le milieu de
est un diamètre du sphère donc et appartiennent à
On dit la sphère de diamètre on note ou .
Propriété
L'équation cartésienne de est :
ou bien
IIX- Étude analytique du sphère
8-4/ L’ensemble des points tel que
On pose
L’ensemble des points tel que est :
- si
- si
- La sphère si
IIX- Étude analytique de la sphère
8-5/ Positions relatives d’une sphère et un plan
Cas 1 :
Cas 2 :
; et sont tangents en avec
Cas 3 :
; coupe suivant le cercle de centre et de rayon
Équation du plan tangent à une sphère
Par un point quelconque d’une sphère il existe un et un seul plan tangente au sphère au point .
L’équation de est :
IIX- Étude analytique de la sphère
8-6/ Positions relatives d’une sphère et une droite
Cas 1 :
Cas 2 :
; et sont tangents en avec
Cas 3 :
coupe en deux points et (Deux points mais pas le segment )
IX- Exercices
9-1/ Exercice 1
Dans l’espace rapporté à un repère orthonormé direct , on considère les points , , et la sphère d’équation :
- Montrer que
- En déduire que est une équation cartésienne du plan .
- Montrer que la sphère a pour centre le point et pour rayon .
- Montrer que , et en déduire que le plan coupe la sphère suivant un cercle .
- Déterminer une représentation paramétrique de la droite passant par le point et orthogonale au plan .
- Montrer que le point B est le centre du cercle .
IX- Exercices
9-2/ Exercice 2
Dans l’espace rapporté à un repère orthonormé direct , on considère le plan passant par le point et dont est un vecteur normal et la sphère de centre le point et de rayon .
- Montrer que est une équation cartésienne du plan .
- Montrer que le plan est tangent à la sphère et vérifier que est le point de contact.
- Déterminer une représentation paramétrique de la droite passant par le point et orthogonale au plan .
- Montrer que la droite est tangente à la sphère au point .
- Montrer que et en déduire l’aire du triangle .
IX- Exercices
9-3/ Exercice 3
L’espace est rapporté à un repère orthonormé direct .
On considère la sphère d’équation et le plan d’équation .
- Montrer que la sphère a pour centre le point et pour rayon .
- Calculer et en déduire que le plan coupe la sphère suivant un cercle .
- Déterminer le centre et le rayon du cercle .
Soit la droite passant par le point et orthogonale au plan .
- Montrer que est un vecteur directeur de la droite .
- Montrer que et en déduire que la droite coupe la sphère en deux points.
- Déterminer les coordonnées de chaque point d’intersection de la droite et de la sphère .
IX- Exercices
9-4/ Exercice 4
Dans l’espace rapporté à un repère orthonormé direct , on considère les points , et .
- Montrer que et en déduire que est une équation cartésienne du plan .
On considère la sphère dont une équation est .
- Vérifier que la sphère a pour centre et pour rayon .
- Vérifier que est une représentation paramétrique de la droite passant par le point et orthogonale au plan .
- Déterminer les coordonnées de point d’intersection de la droite et du plan .
- Vérifier que , puis montrer que le plan coupe la sphère selon un cercle de rayon , dont on déterminera le centre.
IX- Exercices
9-5/ Exercice 5
Dans l’espace rapporté à un repère orthonormé direct , on considère le plan d'équation .
- Les points et appartiennent-ils au plan ?
- Calculer la distance puis les distances de ces deux points et au plan .
- Le point est-il le projeté orthogonal de sur le plan ?
IX- Exercices
9-6/ Exercice 6
On considère les plans d'équations respectives et , et la sphère de centre et tangente au plan .
Soit la droite qui passe par et perpendiculaire au plan .
- Monter que les plans et sont orthogonaux.
- Déterminer l’équation cartésienne de la sphère .
- Déterminer le point de tangence de et .
- Déterminer le point d’intersection de et .
- Montrer que le plan coupe la sphère suivant une cercle dont on déterminera le centre et le rayon.


