Séance 18-B - Chute verticale avec frottement

Sommaire

I- Chute verticale avec frottement

1-1/ Les forces agissantes

1-2/ La force de pesanteur

1-3/ La force de frottement fluide

1-4/ La poussée d'Archimède

1-5/ L’équation différentielle vérifiée par la vitesse

1-6/ Les régimes d’une chute verticale

II- La méthode d’Euler pour la résolution approchée d’une équation différentielle

III- Exercices

3-1/ Exercice 1

3-2/ Exercice 2

3-3/ Exercice 3

3-4/ Exercice 4

I- Chute verticale avec frottement

1-1/ Les forces agissantes

Tous corps immergé dans un fluide est soumis à trois forces :

$\overrightarrow{P}$ : La force de pesanteur (poids du corps).

$\overrightarrow{F_A}$ : La poussée d'Archimède.

$\overrightarrow{f}$ : La force de frottement fluide exercée par le fluide.

I- Chute verticale avec frottement

1-2/ La force de pesanteur

Dans le champ de pesanteur terrestre, tous les solides sont soumis à une force exercée par la terre, c’est le poids du corps.

Le vecteur poids est le produit de la masse $m$ du solide et le vecteur champ de pesanteur terrestre $\overrightarrow{g}$

$\overline{)\overrightarrow{ P}=m\overrightarrow{g} }$

I- Chute verticale avec frottement

1-3/ La force de frottement fluide

On modélise l’ensemble de forces de frottement entre le solide et le fluide par une seule force $\overrightarrow{f}$, c’est la force de frottement fluide.

Il existe plusieurs types de forces de frottement fluide :

• Si le solide est petit et sa vitesse est faible : $\overrightarrow{f}=-h.v.\overrightarrow{k}$
• Si le solide est grand et sa vitesse est grande : $\overrightarrow{f}=-h.v^2.\overrightarrow{k}$

Généralement la force de frottement fluide est de sens opposé à celui du vecteur vitesse et d’intensité : $\overrightarrow{f}=-h.v^n.\overrightarrow{k}$

$h$ est le coefficient de frottement fluide en $Kg.s^{-1}$, il dépend de la forme et le volume du solide, ainsi la nature du fluide et sa viscosité.

I- Chute verticale avec frottement

1-4/ La poussée d'Archimède

Tout solide immergé dans un fluide est soumis à l’action d’une force exercée par ce fluide.

Cette force est appelée poussée d’Archimède, notée $\overrightarrow{F_a}$.

La poussée d’Archimède est égale à l’opposée du vecteur poids du volume du fluide déplacé :

$\overline{)\overrightarrow{ F_a}=-\overrightarrow{P_f}=-m_f\overrightarrow{g} }$

Avec $m_f={\rho }_f.V$ , la masse du fluide déplacé, ${\rho }_f$ la masse volumique du fluide et $V$ son volume déplacé.

D’où les caractéristiques suivantes :

• La direction : Verticale
• Le sens : Vers le haut
• La norme : $F_a={\rho }_f.V.g$

I- Chute verticale avec frottement

1-5/ L’équation différentielle vérifiée par la vitesse

On applique alors la deuxième loi de Newton :

$\sum _{}^{}\overrightarrow{F}=\overrightarrow{P}+\overrightarrow{F_A}+\overrightarrow{f}=m\overrightarrow{a}$

En projetant la relation vectorielle sur l’axe vertical (O,z) dirigé vers le bas :

$$\begin{gathered} P-F_A-f=ma \\ mg-\rho Vg-h{v}^n=ma=\frac{dv}{dt} \end{gathered}$$

L’équation différentielle s’écrit sous la forme :

$\overline{) A-B{v}^n=\frac{dv}{dt} }$

Avec : $A=g\left(1-\frac{\rho V}{m}\right)$ et $B=\frac{h}{m}$.

I- Chute verticale avec frottement

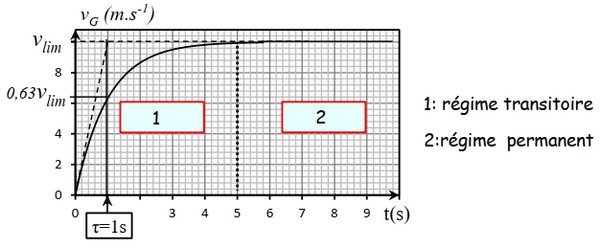
1-6/ Les régimes d’une chute verticale

Au cours d’une chute verticale avec frottement, le mouvement du solide peut se décomposer en deux phase :

1- Le régime initial ou transitoire, pendant lequel :

• La vitesse $v$ augmente.
• La valeur $f$ de la force de frottement fluide augmente.
• L’accélération $a$ diminue.

2- Le régime asymptotique ou permanent, pendant lequel

• La vitesse $v$ est égale à une vitesse constante $v_{\mathcal{l}}$.
• La valeur $f$ de la force de frottement fluide est constante.
• L’accélération $a$ est nulle.

$v_{\mathcal{l}}={\left(\frac{A}{B}\right)}^{\frac{1}{n}}={\left[\frac{g}{k}\left(\rho -{\rho }_f\right).V\right]}^{\frac{1}{n}}$

II- La méthode d’Euler pour la résolution approchée d’une équation différentielle

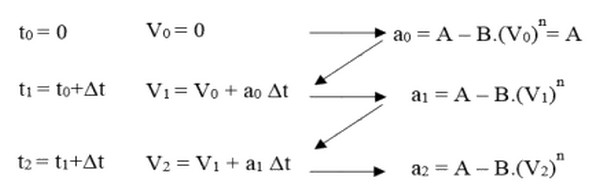
La méthode d'Euler est une méthode itérative (c'est à dire qu'elle nécessite la répétition d'un même calcul),elle permet de savoir la vitesse de la bille à instant donné.

Cette méthode comporte deux étapes de calcul.

La 1ère étape

Si on connaît la vitesse initiale $v_0$, on détermine la valeur de l'accélération initiale $a_0$ à partir de la relation : $a_0=A-B.{v_0}^n$

La 2ème étape

Si on connaît le pas de calcul $\Delta t=t_{i+1}-t_i$, on détermine la vitesse $v_{i+1}$ à l'instant $t_{i+1}$ par la relation suivante :

$v_{i+1}=v_i+a_i\Delta t$

Donc les deux relations intéressantes dans la méthode d'Euler sont : $a_i=A-B.{v_i}^n$ et $v_{i+1}=v_i+a_i\Delta t$

Initialement on connaît la valeur de la vitesse initiale $v_0$ :

Remarque

Le choix du pas du calcul a une grande importance dans la méthode d'Euler, car plus que sa valeur est petite plus les résultats théoriques sont proches des résultats expérimentaux.

On prend généralement un pas de calcul égale à $\Delta t=\frac{\tau }{10}$, pour ne pas dépasser la vitesse limite du solide.

III- Exercices

3-1/ Exercice 1

La grêle se forme dans les cumulo-nimbus situés entre $1000m$ et $10 000m$ d’altitude où la température est très basse, avoisinant les $-40°C$.

Le grêlon tombe lorsqu’il n’est plus maintenu au sein du nuage. Au sol sa vitesse peut atteindre $160km/h$.

On étudie un grêlon de masse $13g$ qui tombe d’un point $O$ d’altitude $1500m$ sans vitesse initiale, il peut être assimilé à une sphère de diamètre $3,0cm$.

Le point $O$ sera pris comme origine d’un axe $Oz$ orienté positivement vers le bas.

L’intensité de la pesanteur sera considérée comme constante et de valeur $g=9,80m.s^{-2}$.

Données :

• Volume d’une sphère $V=\frac{4}{3}\mathrm{\pi }.{\mathrm{r}}^3$
• Masse volumique de l’air $\rho =1,3kg.m^{-3}$

Chute libre

On admettra que le grêlon tombe en chute libre.

1. En appliquant la deuxième loi de Newton, déterminer les équations horaires donnant la vitesse et la position du centre d’inertie $G$ du grêlon en fonction de la durée $t$ de la chute.

2. Calculer la valeur de la vitesse lorsqu’il atteint le sol, ce résultat est-il vraisemblable ? Justifier.

Chute réelle

En réalité le grêlon est soumis à deux autres forces, la poussée d’Archimède $\overrightarrow{F_a}$ et la force de frottement fluide $\overrightarrow{f}$ proportionnelle au carré de la vitesse telle que $f=K.v^2$.

3. Par une analyse dimensionnelle, déterminer l’unité du coefficient $K$ dans le Système International.

4. Donner l’expression de la valeur de la poussée d’Archimède, la calculer et la comparer à celle du poids. Conclure.

On néglige la poussée d’Archimède.

5. Montrer que l’équation différentielle peut s’écrire sous la forme $\frac{dv}{dt}=A-B{v}^2$

On veut résoudre cette équation différentielle par une méthode numérique : la méthode d’Euler.

Le tableau suivant est un extrait d’une feuille de calcul des valeurs de la vitesse $v$ et de l’accélération $a$ en fonction du temps $t$, il correspond aux valeurs $A=9,80 m.s^{-2}$ et $B=1,56\times {10}^{-2} m^{-1}$, avec un pas de variation $\Delta t=0,5s$.

6. Déterminer $a_4$ et $v_5$ en détaillant les calculs.

7. Exprimer littéralement la vitesse limite atteinte par le grêlon en fonction de $A$ et $B$ puis calculer sa valeur numérique.

La courbe d’évolution de la vitesse en fonction du temps est donnée ci-dessous :

8. Retrouver graphiquement la valeur de la vitesse calculée au paragraphe précédent.

III- Exercices

3-2/ Exercice 2

Une bille, de masse $m=7,1g$ et de volume $V=0,91c{m}^3$, est abandonnée sans vitesse initiale dans une huile de masse volumique $\rho =920Kg.m^{-3}$ et de viscosité $\eta$ :

L'huile exerce sur la bille en mouvement une force de frottement $f=k{v}^2$.

L'étude d'un enregistrement de la chute (verticale) de cette bille permet d'obtenir la courbe expérimentale donnant l'évolution de la vitesse de la bille au cours du temps :

1. Faire l'inventaire des forces agissant sur la bille en mouvement dans l'huile.

2. En appliquant deuxième loi de newton monter que l'équation différentielle satisfaite par la vitesse de la bille s’écrit sous la forme $\frac{dv}{dt}=A-B{v}^2$,

3. Détermine l’expression de $A$ et $B$.

4. En déduire l'expression de la vitesse limite de la bille.

5. Déterminer graphiquement la valeur de la vitesse limite $V_{lim}$ et la constante de temps $\tau$; en déduire la valeur de $k$.

Pour une bille le coefficient de frottement est $k=6\mathrm{\pi }\eta r$.

6. En déduire la valeur de la viscosité $\eta$ de l'huile utilisée.

III- Exercices

3-3/ Exercice 3

Pour ne pas abîmer les produits alimentaires suite au choc avec le sol, la caisse est attachée à un parachute lui permettant de descendre lentement.

L’hélicoptère reste immobile à la hauteur précédente $H$ au point $O$.

La caisse tombe verticalement sans vitesse initiale à l’instant $t_0=0$.

L’air exerce sur la caisse des forces de frottement dont l’expression est $\overrightarrow{f}=-100\overrightarrow{V}$. Avec $V$ la vitesse de la caisse à l’instant $t$.

On néglige la poussée d’Archimède pendant la chute.

On donne la masse du système (caisse et le parachute) : $m=150kg$.

1. Trouver dans le référentiel $R\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ l’équation différentielle vérifiée par le centre d’inertie $G$ du système.

La courbe suivante représente la variation de la vitesse de $G$ en fonction du temps :

2. Déterminer la vitesse limite $V_{lim}$ et le temps caractéristique $\tau$ de la chute.

3. Donner une valeur approximative de la durée du régime initial.

4. En utilisant la méthode d’Euler et le tableau suivant, déterminer la valeur de la vitesse $V_4$ et celle de l’accélération $a_4$.

III- Exercices

3-4/ Exercice 4

La charge s’arrête à une hauteur donnée.

À un instant $t=0$, une partie $\left(S\right)$ de masse $m_S=30kg$ de la charge tombe sans vitesse initiale.

On étudie le mouvement du centre d’inertie $G_S$ de la partie $\left(S\right)$ dans le repère $R\left(O,\overrightarrow{j}\right)$, avec l’axe $Oy$ orienté vers le bas :

La position de $G_S$ est confondue avec l’origine de l’axe $Oy$ à l’origine des dates.

On modélise l’action de l’air sur la partie $\left(S\right)$ au cours de son mouvement par la force $\overrightarrow{f}=-k.v^2.\overrightarrow{j}$, avec $v$ le vecteur vitesse de $G_S$ à l’instant $t$, et $k=2,7$ dans le système international des unités.

On néglige l’action de la poussée d’Archimède devant les autres forces exercées sur $\left(S\right)$.

1. En se basant sur l’équation au dimensions, déterminer l’unité de $k$ dans le système international des unités.

2. Montrer que l’équation différentielle vérifiée par la vitesse $v$ s’écrit comme suit : $\frac{dv}{dt}+9.{10}^{-2}{v}^2=9,8$

3. Déterminer la vitesse limite $V_{lim}$ du mouvement.

La vitesse du centre d’inertie $G_S$ à l’instant $t_1$ est $v_1=2,75m.s^{-1}$.

4. Trouver en utilisant la méthode d’Euler sa vitesse $v_2$ à l’instant $t_2=t_1+\Delta t$, où $\Delta t$ est le pas du calcul et $\Delta t=2,4.{10}^{-2}s$.