Étude quantitative de la variation (La biométrie) - Cours (Partie 2)

Sommaire

III- Les paramètres caractéristiques d’une distribution de fréquence

3-1/ Les paramètres de position

3-2/ Les paramètres de dispersion

III- Les paramètres caractéristiques d’une distribution de fréquence

3-1/ Les paramètres de position

Le mode

Dans le cas d’une variation discontinue c’est la valeur de la variable qui correspond à la fréquence la plus élevée .

Dans une variation continue, le mode est la valeur moyenne de la classe ayant la plus grande fréquence.

Le mode permet de déterminer l’homogénéité de la distribution d’une variable :

• Si le polygone de fréquence est unimodale, l’échantillon étudié est homogène
• Si le polygone de fréquence est bimodale, ou plurimodale, l’échantillon étudié est hétérogène.

III- Les paramètres caractéristiques d’une distribution de fréquence

3-1/ Les paramètres de position

La moyenne arithmétique $\overline{\mathrm{X}}$ (lire X barre)

Elle nous renseigne sur la valeur centrale du variable tenant compte des effectifs. Elle est calculée par la suivante :

$\overline{)\mathrm{ }\overline{\mathrm{X}}\mathrm{=}\frac{\mathrm{\sum }_{\mathrm{1}}^{\mathrm{i}}\left(f_i{x}_i\right)}{\mathrm{n}}\mathrm{ }}$

Avec :

• $x_i$ : la valeur de la variable (dans une variation discontinue) ou le centre de la classe (dans une variation continue).
• $f_i$ : la fréquence de la variable.
• $n$ : le nombre total d’individus dans la population étudiée.

III- Les paramètres caractéristiques d’une distribution de fréquence

3-1/ Les paramètres de position

Application 1

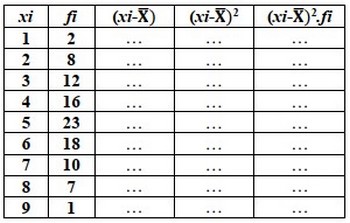
Calculer $\overline{X}$ pour la distribution de nombre de nouveau nés chez les femelles de souris :

III- Les paramètres caractéristiques d’une distribution de fréquence

3-1/ Les paramètres de position

Application 2

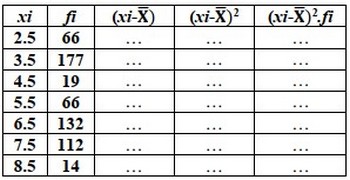
Calculer $\overline{X}$ pour la distribution de la longueur des pinces :

III- Les paramètres caractéristiques d’une distribution de fréquence

3-2/ Les paramètres de dispersion

La variance (V)

La variance est un paramètre permettant de mesurer le degré de dispersion d’une distribution.

La variance se calcule par la formule suivante :

$\boxed{\mathrm{ }\mathrm{V}\mathrm{=}\frac{\mathrm{\sum }_{\mathrm{1}}^{\mathrm{i}}{\mathrm{f}}_{\mathrm{i}}{\mathrm{(}{\mathrm{x}}_{\mathrm{i}}\mathrm{-}\overline{\mathrm{X}}\mathrm{)}}^{\mathrm{2}}}{\mathrm{n}}\mathrm{ }}$

III- Les paramètres caractéristiques d’une distribution de fréquence

3-2/ Les paramètres de dispersion

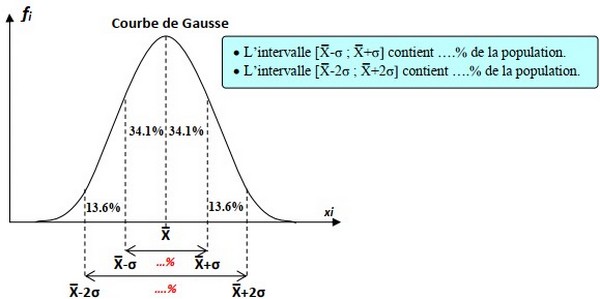
L’écart type (σ)

$\boxed{\mathrm{ }\mathit{\sigma }\mathrm{=}\sqrt{\mathrm{V}}\mathrm{=}\sqrt{\frac{\mathrm{\sum }_{\mathrm{1}}^{\mathrm{i}}{\mathrm{f}}_{\mathrm{i}}{\mathrm{(}{\mathrm{x}}_{\mathrm{i}}\mathrm{-}\overline{\mathrm{X}}\mathrm{)}}^{\mathrm{2}}}{\mathrm{n}}}\mathrm{ }}$

Plus l’écart type est grand, plus les valeurs sont dispersées, et plus l’homogénéité de la population diminue

L’écart type permet de définir ce qu’on appelle le domaine de confiance.

III- Les paramètres caractéristiques d’une distribution de fréquence

3-2/ Les paramètres de dispersion

L’écart type (σ)

III- Les paramètres caractéristiques d’une distribution de fréquence

3-2/ Les paramètres de dispersion

Application 1

Calculer l’écart type dans la distribution du nombre de nouveau nés chez les femelles de souris :

III- Les paramètres caractéristiques d’une distribution de fréquence

3-2/ Les paramètres de dispersion

Application 2

Calculer l’écart type dans la distribution de la longueur des pinces :