Séance 2 - Les ondes mécaniques progressives périodiques

Sommaire

I- Ondes mécaniques progressives périodiques

1-1/ Définition

1-2/ Exemples

II- Exemples d’ondes mécaniques progressives périodiques

2-1/ Onde progressive le long d'une corde

2-2/ Onde progressive à la surface de l'eau

2-3/ Ondes sonores et ultrasonores

III- Détermination expérimentale de la vitesse de propagation

3-1/ Comparaison du mouvement de deux points du milieu de propagation

3-2/ Expérience des deux microphones

IV- Phénomène de diffraction

4-1/ Définition

4-2/ Onde diffractée à la surface de l'eau

V- Exercices

5-1/ Exercice 1

5-2/ Exercice 2

5-3/ Exercice 3

5-4/ Exercice 4

I-  Ondes mécaniques progressives périodiques

1-1/ Définition

Une onde est périodique si elle se répète identiquement à elle-même pendant des mêmes intervalles de temps appelés période T.

Elle est dite sinusoïdale si sa variation est une sinusoïde en fonction du temps et l'élongation d'un point du milieu de propagation s'écrit de la manière suivante :

$\overline{)\mathrm{x}\left(t\right)\mathrm{=}\mathrm{A}\mathrm{c}\mathrm{o}\mathrm{s}(\frac{2\pi }{T}t+\phi )}$

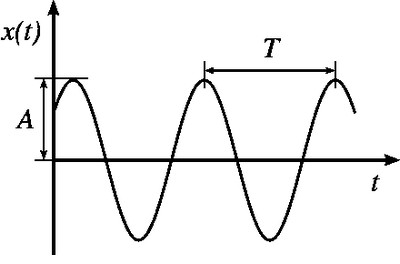• x(t) : L’élongation à un instant t. (m)
• A : L'amplitude (élongation maximale). (m)
• T : La période (périodicité temporaire). (s)
• $\mathrm{\phi }$ : La phase à l'origine, elle se détermine à partir des conditions initiales. (rad)

1-2/ Exemples

II- Exemples d’ondes mécaniques progressives périodiques

2-1/ Onde progressive le long d'une corde

Expérience

On utilise une corde élastique tendue horizontalement par un corps suspendu comme l'indique la figure suivante.

La corde est attachée en S au bout d'une lame vibrante dont le mouvement est entretenu par un électro-aimant alimenté par un courant alternatif.

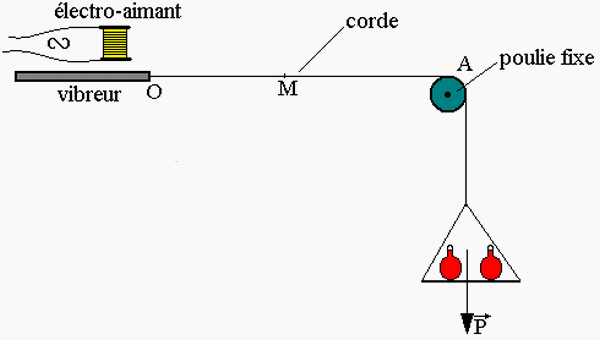
Définition de la longueur d'onde

$\overline{)\mathrm{\lambda }\mathrm{=}\mathrm{\nu }\mathrm{T}\mathrm{=}\frac{\mathrm{\nu }}{\mathrm{\upsilon }}}$

II- Exemples d’ondes mécaniques progressives périodiques

2-2/ Onde progressive à la surface de l'eau

Onde circulaire

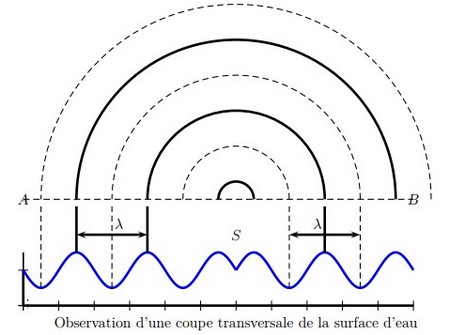
Onde rectiligne

II- Exemples d’ondes mécaniques progressives périodiques

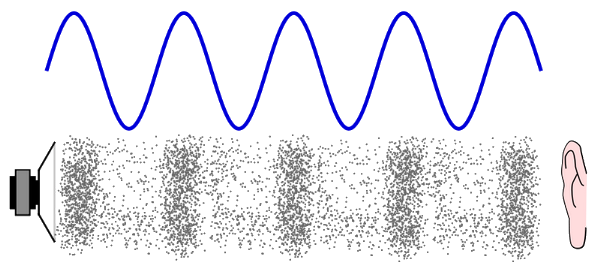
2-3/ Ondes sonores et ultrasonores

Ondes sonores

Les ondes sonores sont des ondes mécaniques longitudinales qui se produisent lorsque la vibration d'un corps se propage dans un milieu environnant.

La célérité d’une onde sonore est d’autant plus grande que la densité du milieu est élevée

$\overline{){\mathrm{\nu }}_{\mathrm{g}\mathrm{a}\mathrm{z}}\mathrm{<}{\mathrm{\nu }}_{\mathrm{l}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{d}\mathrm{e}}\mathrm{<}{\mathrm{\nu }}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{e}}}$

Ondes ultrasonores

Les ondes ultrasonores sont des ondes sonores dont la fréquence est supérieure à 20kHz, ils sont inaudibles et ils se réfléchissent partiellement sur un obstacle.

III- Détermination expérimentale de la vitesse de propagation

3-1/ Comparaison du mouvement de deux points du milieu de propagation

• On a ${\mathrm{M}}_{\mathrm{1}}{\mathrm{M}}_{\mathrm{3}}\mathrm{=}\mathrm{2}\mathrm{\lambda }$ donc ${\mathrm{M}}_{\mathrm{1}}$ et ${\mathrm{M}}_3$ vibrent en phase
• On a ${\mathrm{M}}_{\mathrm{1}}{\mathrm{M}}_{\mathrm{4}}\mathrm{=}\mathrm{3}\mathrm{\lambda }$ donc ${\mathrm{M}}_{\mathrm{1}}$ et ${\mathrm{M}}_4$ vibrent en phase

 En général, deux points M et M' du milieu de propagation vibrent en phase si la distance qui les sépare est un multiple de la longueur d'onde : $\overline{)\mathrm{M}\mathrm{M}\mathrm{\text{'}}\mathrm{=}\mathrm{k}\mathrm{.}\mathrm{\lambda }\mathrm{ }(k\in \mathbb{N}*)}$

• On a ${\mathrm{M}}_{\mathrm{1}}{\mathrm{M}}_{\mathrm{1}}\mathrm{\text{'}}\mathrm{=}\raisebox{1ex}{$\mathrm{\lambda }$}\!\left/ \!\raisebox{-1ex}{$\mathrm{2}$}\right.$ donc ${\mathrm{M}}_{\mathrm{1}}$ et ${\mathrm{M}}_{\mathrm{1}}\mathrm{\text{'}}$ vibrent en opposition de phase
• On a ${\mathrm{M}}_{\mathrm{1}}{\mathrm{M}}_{\mathrm{3}}\mathrm{\text{'}}\mathrm{=}\mathrm{5}\mathrm{.}\raisebox{1ex}{$\mathrm{\lambda }$}\!\left/ \!\raisebox{-1ex}{$\mathrm{2}$}\right.$ donc ${\mathrm{M}}_{\mathrm{1}}$ et ${\mathrm{M}}_{\mathrm{3}}\mathrm{\text{'}}$ vibrent en opposition de phase

  En général, deux points M et M' du milieu de propagation vibrent en opposition de phase si la distance qui les sépare est un nombre impair de la demi-longueur d'onde : $\overline{)\mathrm{MM}\mathrm{\text{'}}\mathrm{=}\mathrm{(}\mathrm{2}\mathrm{k}\mathrm{+}\mathrm{1}\mathrm{)}\mathrm{.}\raisebox{1ex}{$\mathrm{\lambda }$}\!\left/ \!\raisebox{-1ex}{$\mathrm{2}$}\right.\mathrm{ }\mathrm{(}\mathrm{k}\mathrm{\in }\mathrm{\mathbb{N}}\mathrm{*}\mathrm{)}}$

III- Détermination expérimentale de la vitesse de propagation

3-2/ Expérience des deux microphones

Pour déterminer la vitesse de propagation du son émis par un haut-parleur dans l'air on utilise le montage suivant :

Après avoir activé le haut parleur on visualise sur l'écran de l'oscilloscope le signal correspondant à chacun des microphones M1 et M2.

Lorsque les deux microphones sont placés côte à côte face au haut parleur et à la même distance de lui, les deux signaux correspondant à M1 et à M2 sont en phase.

Pour un son de fréquence de 103Hz émis, on laisse le microphone M1 à sa place et on déplace le microphone M2 lentement et parallèlement à l'axe du haut-parleur.

On indique la distance d chaque fois que les deux signaux sont en phase et on obtient les résultats suivants : 34cm – 68cm – 102cm – 136cm.

Or deux points du milieu de propagation vibrent en phase si la distance qui les sépare est un multiple de la longueur d'onde : $\overline{)\mathrm{d}\mathrm{=}\mathrm{k}\mathrm{.}\mathrm{\lambda }}$

Donc la longueur de l'onde sonore émise par le haut-parleur est : $\overline{)\mathrm{\lambda }\mathrm{=}\mathrm{34}\mathrm{ }\mathrm{cm}}$

IV- Phénomène de diffraction

4-1/ Définition

Le phénomène de diffraction est caractéristique des ondes. Il se manifeste lorsque les dimensions d'une ouverture ou d'un obstacle sont inférieures ou de l'ordre de grandeur de la longueur d'onde: $\left(a\approx \lambda \right)$.

C'est la modification de la forme d'une onde passant par une ouverture de largeur $a\le \lambda$.

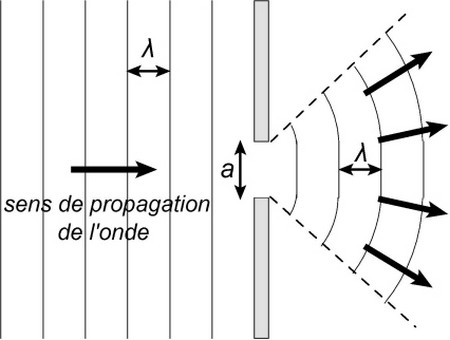
IV- Phénomène de diffraction

4-2/ Onde diffractée à la surface de l'eau

On utilise une cuve à onde munie d'une plaque vibrante devant laquelle on place un diaphragme comportant une ouverture de largeur a.

V– Exercices

5-1/ Exercice 1

À l’aide d’un vibreur S, on crée des ondes progressives sinusoïdales de fréquence f à la surface de l’eau :

Les pointe A et B sont distants d’une distance d = 6,0 cm.

1) Représenter sur la figure la longueur d’onde.

2) Déterminer précisément cette longueur d’onde.

3) Sachant que la fréquence des vibrations vaut f =17Hz, calculer la célérité de l’onde.

4) On dispose un petit morceau de liège (supposés ponctuels) au point M (SM = 8,5 cm). Comparer le mouvement du vibreur avec petit morceau de liège.

V– Exercices

5-2/ Exercice 2

Pour déterminer la vitesse de propagation du son dans l'air, on a réalisé le montage expérimental de la figure (1),dans lequel les deux microphones sont séparés par une distance $\mathrm{d}$.

Les deux signaux représentés dans la figure (2) représentent la tension entre les bornes de chaque microphone pour une distance ${\mathrm{d}}_{\mathrm{1}}\mathrm{=}\mathrm{41}\mathrm{c}\mathrm{m}$ :

La sensibilité horizontale utilisée pour les deux entrées est : $\mathrm{0}\mathrm{,}\mathrm{1}\mathrm{m}\mathrm{s}\mathrm{/}\mathrm{d}\mathrm{i}\mathrm{v}$

• Déterminer à partir de figure (2) la période $\mathrm{T}$ de l'onde sonore émise par le haut parleur.

On déplace horizontalement le microphone ${\mathrm{R}}_{\mathrm{2}}$ selon la ligne $\mathrm{\Delta }$ jusqu'à ce que les deux signaux soient de nouveau en phase pour la première fois et la distance entre ${\mathrm{R}}_{\mathrm{1}}$ et ${\mathrm{R}}_{\mathrm{2}}$ soit : ${\mathrm{d}}_{\mathrm{2}}\mathrm{=}\mathrm{61}\mathrm{,}\mathrm{5}\mathrm{c}\mathrm{m}$.

• Déterminer la valeur de longueur $\mathrm{\lambda }$ de l'onde sonore.
• Calculer la vitesse $\mathrm{V}$ de propagation de l'onde sonore dans l'air.

V– Exercices

5-3/ Exercice 3

Une plaque verticale $\mathrm{P}$ lié à un vibreur de fréquence $\mathrm{N}\mathrm{=}\mathrm{50}\mathrm{H}\mathrm{z}$ provoque des ondes rectilignes progressives et sinusoïdales sur la surface libre de l'eau dans une cuve à ondes qui se propages sans réflexion ni amortissement.

La figure (1) représente l'aspect de la surface libre de l'eau à un instant donnée pour $\mathrm{d}\mathrm{=}\mathrm{15}\mathrm{m}\mathrm{m}$.

1. Préciser en utilisant la figure (1) la valeur de $\mathrm{\lambda }$

2. Déduire la valeur de $\mathrm{V}$, la vitesse de propagation de l'onde à la surface de l'eau.

On considère le point $\mathrm{M}$ du milieu de propagation (figure 1).

3. Calculer la valeur de $\mathrm{\tau }$, le retard temporel de vibration de $\mathrm{M}$ par rapport à celui de la source $\mathrm{S}$.

On multiple la fréquence du vibreur $(N\text{'}=2N)$ et la longueur de l'onde devient $\mathrm{\lambda }\mathrm{\text{'}}\mathrm{=}\mathrm{3}\mathrm{m}\mathrm{m}$.

4. Calculer, dans ce cas, la valeur $\mathrm{V}\mathrm{\text{'}}$ de la vitesse de propagation de l'onde à la surface de l'eau.

5. L'eau est-il un milieu dispersif ? Justifier votre réponse.

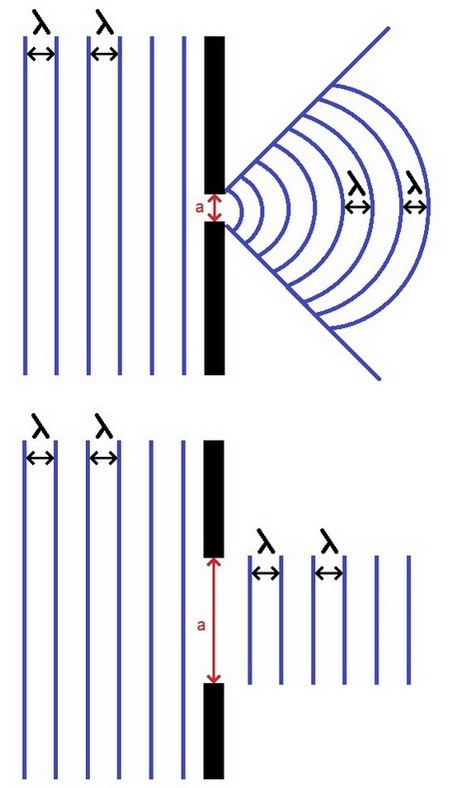
On règle de nouveau la fréquence du vibreur sur la valeur $\mathrm{N}\mathrm{=}\mathrm{50}\mathrm{H}\mathrm{z}$ et on pose dans la cuve à onde deux plaques verticales formant un obstacle contenant une ouverture de largeur $\mathrm{a}$ (figure2) :

6. Représenter en justifiant votre réponse l'aspect de la surface de l'eau après que l'onde dépasse l'obstacle dans chacun des cas suivants : $\mathrm{a}\mathrm{=}\mathrm{4}\mathrm{m}\mathrm{m}$ et $\mathrm{a}\mathrm{=}\mathrm{10}\mathrm{m}\mathrm{m}$.

V– Exercices

5-4/ Exercice 4

Pour déterminer la valeur approximative de la célérité ${\mathrm{V}}_{\mathrm{p}}$ d’une onde ultrasonore dans le pétrole liquide, on réalise l’expériance suivante :

Dans une cuve contenant du pétrole, on fixe à l’une de ses éxtrimités deux émeeurs ${\mathrm{E}}_{\mathrm{1}}$ et ${\mathrm{E}}_{\mathrm{2}}$ qui sont reliés à un générateur GBF.

A l’instante ${\mathrm{t}}_{\mathrm{0}}\mathrm{=}\mathrm{0}$, les deux émettent chacun une onde ultrasonore, une se propage dans l’air et l’autre dans le pétrole.

A l’autre extrémité de la cuve, on place deux récepteurs ${\mathrm{R}}_{\mathrm{1}}$ et ${\mathrm{R}}_{\mathrm{2}}$, l’un dans l’air et l’autre dans le pétrole.

Les récepteurs sont à une distance L des émetteurs. (voir figure 1)

On visualise sur l’écran d’un oscilloscope les deux signaux reçus par ${\mathrm{R}}_{\mathrm{1}}$ et ${\mathrm{R}}_{\mathrm{2}}$. (voir figure 2)

Données :

• Les deux ondes parcourent la même distance : $\mathrm{L}\mathrm{=}\mathrm{1}\mathrm{,}\mathrm{84}\mathrm{ }\mathrm{m}$
• La célérité des ultrasons dans l’air : ${\mathrm{V}}_{\mathrm{a}\mathrm{i}\mathrm{r}}\mathrm{=}\mathrm{340}\mathrm{ }\mathrm{m}\mathrm{.}{\mathrm{s}}^{\mathrm{-}\mathrm{1}}$
• La sensibilité horizontale del’oscilloscope : $\mathrm{2}\mathrm{ }\mathrm{m}\mathrm{s}\mathrm{/}\mathrm{d}\mathrm{i}\mathrm{v}$

1) Les ondes ulrasonores, sont-elles longitudinales ou transversales ? justifier

2) On exploitant la figure 2 , déterminer la valeur du retard temporel entre les deux ondes reçues

3) Montrer que l’expression de $\mathrm{\tau }$ s’écrit sous la forme : $\mathrm{\tau }\mathrm{=}\mathrm{L}(\frac{1}{V_{air}}-\frac{1}{V_p})$

4) Trouver la valeur approchée de la célérité ${\mathrm{V}}_{\mathrm{p}}$