Séance 11 - Triangles

Sommaire

I- Somme des mesures des angles d’un triangle

1-1/ Règle

II- Triangles particuliers

2-1/ Le triangle rectangle

2-2/ Le triangle isocèle

2-3/ Le triangle équilatéral

2-4/ Le triangle rectangle isocèle

III- Exercices

3-1/ Exercice 1

3-2/ Exercice 2

3-3/ Exercice 3

3-4/ Exercice 4

3-5/ Exercice 5

3-6/ Exercice 6

3-7/ Exercice 7

I- Somme des mesures des angles d’un triangle

1-1/ Règle

La somme des mesures des angles d’un triangle est égale à 180°

Exemple

ABC est un triangle:

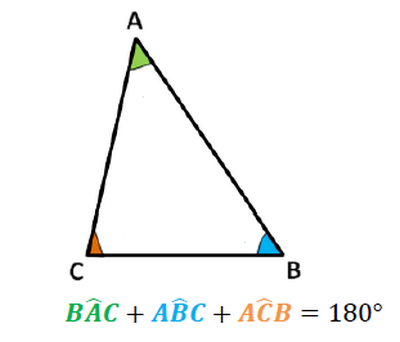
II- Triangles particuliers

2-1/ Le triangle rectangle

Définition

Le triangle rectangle est un triangle qui a un angle droit

Exemple

ABC est un triangle rectangle en A.

Le côté opposé à l’angle droit s’appelle l’hypoténuse : c’est le plus grand des trois côtés du triangle.

Propriété directe

Les angles aigus d’un triangle rectangle sont complémentaires.

Propriété réciproque

Si un triangle possède deux angles complémentaires alors il est rectangle.

II- Triangles particuliers

2-2/ Le triangle isocèle

Définition

Le triangle isocèle est un triangle qui a deux côtés égaux.

Exemple

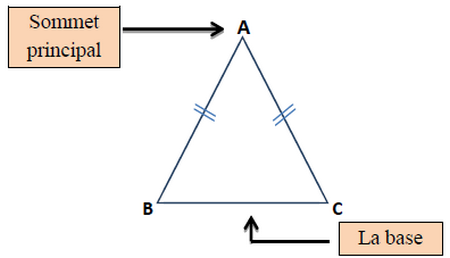
ABC est un triangle isocèle en A

Donc : AB=AC

Propriété directe

Dans un triangle isocèle, les angles à la base sont égaux.

Propriété réciproque

Si un triangle a deux angles isométriques (égaux), alors c’est un triangle isocèle.

II- Triangles particuliers

2-3/ Le triangle équilatéral

Définition

Le triangle équilatéral est un triangle qui a ses trois côtés égaux.

Exemple

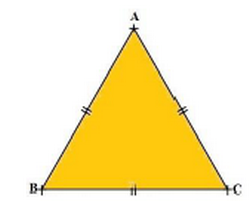
ABC est un triangle équilatéral

Donc : AB = AC = BC

Propriété directe

 Si un triangle est équilatéral alors chaque angle mesure 60°.

Propriété réciproque

Si un triangle est isocèle possède un angle de mesure 60° alors c’est un triangle équilatéral.

II- Triangles particuliers

2-4/ Le triangle rectangle isocèle

Définition

Le triangle rectangle isocèle est un triangle qui a un angle droit et deux côtés égaux.

Exemple

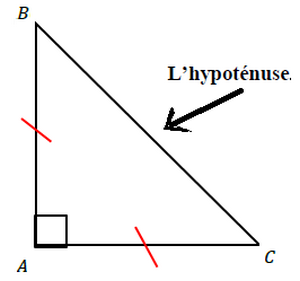
ABC est un triangle rectangle isocèle

Donc : $\mathrm{B}\overbrace{\mathrm{A}}\mathrm{C}\mathrm{=}\mathrm{90}\mathrm{°}$ et AB = AC

Propriété directe

Si un triangle est rectangle isocèle, alors ses angles aigus sont isométriques (égaux) et leur mesure est égale à 45°.

Propriété réciproque

Si un triangle a deux angles isométriques (égaux) et leur mesure est égale à 45°, alors c’est un triangle rectangle isocèle.

III- Exercices

3-1/ Exercice 1

ABC est un triangle rectangle en A

Reproduis et complète le tableau suivant :

III- Exercices

3-2/ Exercice 2

On donne le triangle EFG tel que : $\mathrm{E}\overbrace{\mathrm{F}}\mathrm{G}\mathrm{ }\mathrm{=}\mathrm{ }\mathrm{20}\mathrm{°}$ et $\mathrm{G}\overbrace{\mathrm{E}}\mathrm{F}\mathrm{ }\mathrm{=}\mathrm{ }\mathrm{70}\mathrm{°}$

Déterminer la nature du triangle EFG.

III- Exercices

3-3/ Exercice 3

1) Préciser la nature d’un triangle possédant un angle mesurant 26° et un autre angle mesurant 64°.

2) Préciser la nature d’un triangle possédant un angle mesurant 23° et un autre angle mesurant 134°.

III- Exercices

3-4/ Exercice 4

Observe les codages de la figure suivante puis calcule la mesure de l'angle $\mathrm{I}\hat{\mathrm{O}}\mathrm{S}$.

III- Exercices

3-5/ Exercice 5

En utilisant les indications portées sur la figure, déterminer les mesures de tous les angles.

III- Exercices

3-6/ Exercice 6

On considère la figure suivante :

1. Déterminer la nature du triangle $IBF$, en déduire la mesure de $\widehat{BIF}$.

2. Déterminer la nature du triangle $AIE$, en déduire la mesure de $\widehat{AIE}$.

3. Montrer que les points $A$, $I$ et $B$ sont alignés.

III- Exercices

3-7/ Exercice 7

On considère la figure suivante :

1. Déterminer la nature de chacun des triangles $HEF$, $EFG$ et $EGI$.

2. Calculer la mesure de l'angle $\widehat{HEI}$.

3. Déterminer la mesure des angles $\widehat{EHF}$ et $\widehat{EIG}$.

4. Comparer les deux angles $\widehat{HFG}$ et $\widehat{FGI}$.