Séance 8 - Équations, inéquations et systèmes

Sommaire

I- Rappels

1-1/ Équations du 1er degré à une inconnue

1-2/ Inéquations du 1er degré à une inconnue

II- Équations du second degré à une inconnue

2-1/ Définition

2-2/ Forme canonique du trinôme de second degré $a{x}^2+bx+c \left(a\ne 0\right)$

2-3/ Détermination des solutions de l’équation $a{x}^2+bx+c \left(a\ne 0\right)$

2-4/ La somme et le produit des racines de l’équation $a{x}^2+bx+c \left(a\ne 0\right)$

2-5/ Factorisation et signe du trinôme de second degré $a{x}^2+bx+c \left(a\ne 0\right)$

III- Équations et inéquations du 1er degré à deux inconnues (Méthode graphique)

IV- Déterminants d’un système de deux équations du 1er degré à deux inconnues

4-1/ Définition

4-2/ Propriétés

V- Exercices

5-1/ Exercice 1

5-2/ Exercice 2

5-3/ Exercice 3

5-4/ Exercice 4

I- Rappels

1-1/ Équations du 1er degré à une inconnue

Définition

Soient $a,b\in \mathrm{ℝ} ; \left(a\ne 0\right)$.

Toute équation dont l'écriture se ramène sous la forme suivante $ax+b=0$  avec $x\in \mathrm{ℝ}$  est appelée équation du 1er degré d’un seul inconnu $x$ de et ses coefficients réels sont $a$ et $b$.

Exemple

I- Rappels

1-2/ Inéquations du 1er degré à une inconnue

Définition

Soient $a,b\in \mathrm{ℝ} ; \left(a\ne 0\right)$.

Toute inéquation dont l'écriture se ramène sous la forme suivante $ax+b\ge 0$ ou  $ax+b\le 0$    $ax+b>0$ ou $ax+b<0$ est appelée inéquation du 1er degré d’un seul inconnu $x$.

Signe du binôme du 1er degré $ax+b$

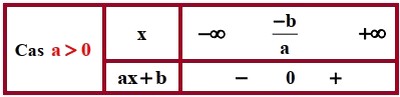
Exemple

II- Équations du second degré à une inconnue

2-1/ Définition

Soient $a,b,c\in \mathrm{ℝ} ; \left(a\ne 0\right)$.

Toute équation dont l'écriture se ramène sous la forme suivante $a{x}^2+bx+c=0$  avec $x\in \mathrm{ℝ}$est appelée équation du 2ème  degré d’un seul inconnu $x$ de et ses coefficients réels sont $a$ et $b$ et $c$.

Exemple

II- Équations du second degré à une inconnue

2-2/ Forme canonique du trinôme de second degré $a{x}^2+bx+c \left(a\ne 0\right)$

L’ écriture $a\left[{\left(x+\frac{b}{2a}\right)}^2-\frac{b^2-4ac}{4a^2}\right]$ est appelée la forme canonique du trinôme de second degré $a{x}^2+bx+c \left(a\ne 0\right)$.

Le nombre $b^2-4ac$ est appelé le discriminant du trinôme de second degré $a{x}^2+bx+c$,  noté par $\Delta$, et on écrit $\Delta =b^2-4ac$.

La forme canonique du trinôme de second degré $a{x}^2+bx+c$ s’écrit :

$a\left[{\left(x+\frac{b}{2a}\right)}^2-\frac{b^2-4ac}{4a^2}\right]=a\left[{\left(x+\frac{b}{2a}\right)}^2-\frac{\Delta }{4a^2}\right]$

d’où :

$a{x}^2+bx+c=a\left[{\left(x+\frac{b}{2a}\right)}^2-\frac{\Delta }{4a^2}\right]$

Exemple

II- Équations du second degré à une inconnue

2-3/ Détermination des solutions de l’équation $a{x}^2+bx+c \left(a\ne 0\right)$

Soit l’équation $a{x}^2+bx+c=0$, et son discriminant $\Delta =b^2-4ac$.

- Si $\Delta >0$, l’équation admet deux solutions distinctes (ou deux racines distinctes) dans $\mathrm{ℝ}$ : $x_1=\frac{-b+\sqrt{\Delta }}{2a}$ et $x_2=\frac{-b-\sqrt{\Delta }}{2a}$.

- Si $\Delta =0$, l’équation admet une solution (solution double) dans $\mathrm{ℝ}$ : $x_0=-\frac{b}{2a}$.

- Si $\Delta <0$, l’équation n’a pas de solution dans $\mathrm{ℝ}$ : $S=\varnothing$.

Exemple

II- Équations du second degré à une inconnue

2-4/ La somme et le produit des racines de l’équation $a{x}^2+bx+c \left(a\ne 0\right)$

Si l’équation  admet deux racines distinctes $x_1$ et $x_2$, alors on a :

$x_1+x_2=-\frac{b}{a}$    et       $x_1\times x_2=\frac{c}{a}$

Exemple

II- Équations du second degré à une inconnue

2-5/ Factorisation et signe du trinôme de second degré    $a{x}^2+bx+c \left(a\ne 0\right)$

Factorisation du trinôme de second degré $a{x}^2+bx+c \left(a\ne 0\right)$

$\Delta$ est le discriminant de l’équation $x\in \mathrm{ℝ}/a{x}^2+bx+c$.

- Si $\Delta >0$, l’équation admet deux solutions distinctes $x_1$ et $x_2$, on a $a{x}^2+bx+c =a\left(x-x_1\right)\left(x-x_2\right)$.

- Si $\Delta =0$, l’équation admet une solution $x_1=-\frac{b}{a}$, on a $a{x}^2+bx+c =a{\left(x-x_1\right)}^2$

- Si $\Delta <0$, l’équation n’a pas de solution dans $\mathrm{ℝ}$, on ne peut pas factoriser $a{x}^2+bx+c$ sous forme de produit de deux polynômes de 1er degré (deux monômes).

Exemple

II- Équations du second degré à une inconnue

2-5/ Factorisation et signe du trinôme de second degré $a{x}^2+bx+c \left(a\ne 0\right)$

Signe du trinôme de second degré $a{x}^2+bx+c \left(a\ne 0\right)$

$\Delta$ est le discriminant de l’équation $x\in \mathrm{ℝ}/a{x}^2+bx+c$.

- Si $\Delta >0$ :

- Si $\Delta =0$ :

- Si $\Delta <0$ : le trinôme n’a pas de racine dans $\mathrm{ℝ}$, on ne peut pas factoriser $a{x}^2+bx+c$, et son signe est celui de a pour tout x de $\mathrm{ℝ}$.

Exemple

III- Équations et inéquations du 1er degré à deux inconnues (Méthode graphique)

Méthode

IV- Déterminants d’un système de deux équations du 1er degré à deux inconnues

4-1/ Définition

On considère le système suivant : $\left(S\right) : \left(x,y\right)\in {\mathrm{ℝ}}^2 / \left\{\begin{array}{l}ax+by=c\\ a\text{'}x+b\text{'}y=c\text{'}\end{array}\right.$.

Le nombre $\Delta =\left|\begin{array}{cc}a& b\\ a\text{'}& b\text{'}\end{array}\right|=ab\text{'}-a\text{'}b$ est appelé le déterminant du système $\left(S\right)$.

Le nombre ${\Delta }_x=\left|\begin{array}{cc}c& b\\ c\text{'}& b\text{'}\end{array}\right|=cb\text{'}-c\text{'}b$ est appelé le déterminant pour déterminer $x$.

Le nombre ${\Delta }_y=\left|\begin{array}{cc}a& c\\ a\text{'}& c\text{'}\end{array}\right|=ac\text{'}-a\text{'}c$ est appelé le déterminant pour déterminer $y$.

Exemple

IV- Déterminants d’un système de deux équations du 1er degré à deux inconnues

4-2/ Propriétés

1. Cas 1 : $\Delta =\left|\begin{array}{cc}a& b\\ a\text{'}& b\text{'}\end{array}\right|=ab\text{'}-a\text{'}b\ne 0$

Le système est appelé système de Cramer, le système admet une solution unique : $S=\left\{\left(\frac{{\Delta }_x}{\Delta },\frac{{\Delta }_y}{\Delta }\right)\right\}$

2. Cas 2 : $\Delta =\left|\begin{array}{cc}a& b\\ a\text{'}& b\text{'}\end{array}\right|=ab\text{'}-a\text{'}b=0$

- Si ${\Delta }_x\ne 0$ ou ${\Delta }_y\ne 0$, le système n’a pas de solution, d’où $S=\varnothing$.

- Si ${\Delta }_x=0$ et ${\Delta }_y=0$, le système se ramène a une seule équation, on prend une par exemple $\left(S\right) : \left(x,y\right)\in {\mathrm{ℝ}}^2/ax+by=c$, le système a une infinité de solutions, d’où ($S=\left\{\left(x,y\right)/y=-\frac{b}{a}x+\frac{c}{a},x\in \mathrm{ℝ}\right\}$

Exemple

V- Exercices

5-1/ Exercice 1

1. Résoudre dans $\mathrm{ℝ}$ les équations suivantes :

$$\begin{gathered} \overline{)1} \frac{2x+3}{x-2}=0 \\ \overline{)2} \frac{x-3}{9x+6}=1 \\ \overline{)3} \frac{4}{x-3}-\frac{5}{x+1}=0 \\ \overline{)4} \frac{2}{x+3}=\frac{x-3}{2} \\ \overline{)5} \frac{x+1}{5x-7}=\frac{5x+7}{x-1} \end{gathered}$$

2. Résoudre dans $\mathrm{ℝ}$ les inéquations suivantes :

$$\begin{gathered} \overline{)1} \left(1-\sqrt{2}\right)x-5\le 0 \\ \overline{)2} 3x-5<7-\sqrt{2}x \\ \overline{)3} \frac{7x-2}{1-\sqrt{3}}\le \frac{7x+2}{1+\sqrt{3}} \\ \overline{)4} \left|x-5\right|<\frac{1}{2} \\ \overline{)5} \left|x+2\right|-5\le 4 \\ \overline{)6} \left|3x-2\right|>3 \end{gathered}$$

V- Exercices

5-2/ Exercice 2

1. Résoudre dans $\mathrm{ℝ}$ les équations suivantes :

$$\begin{gathered} \overline{)1} x^2+x+1=0 \\ \overline{)2} 3x^2+3\sqrt{2}x+2=0 \\ \overline{)3} x^2-x-12=0 \\ \overline{)4} 3x^2+5x+1=0 \\ \overline{)5} 4x^2-3x+1=0 \\ \overline{)6} x^2-x+\frac{1}{4}=0 \end{gathered}$$

2. Résoudre dans $\mathrm{ℝ}$ les inéquations suivantes :

$$\begin{gathered} \overline{)1} x^2-5x+6\le 0 \\ \overline{)2} -x^2+x+6>0 \\ \overline{)3} \left(x^2-5x+6\right)\left(-x^2+x+6\right)\le 0 \\ \overline{)4} \frac{x^2-6x+5}{x^2-4}\ge 0 \\ \overline{)5} \left(x^2+3x+2\right)\left(-x^2+5x-6\right)\le 0 \end{gathered}$$

V- Exercices

5-3/ Exercice 3

1. Résoudre dans ${\mathrm{ℝ}}^2$ les systèmes suivants :

$$\begin{gathered} \overline{)1} \left(S_1\right):\left\{\begin{array}{l}5x-2y=1\\ -10x+4y=3\end{array}\right. \\ \overline{)2} \left(S_2\right):\left\{\begin{array}{l}3x+y=7\\ 2x-y=8\end{array}\right. \end{gathered}$$

2. Résoudre dans ${\mathrm{ℝ}}^2$ le système suivant :

$\left(S\right):\left\{\begin{array}{l}-x+3y=4\\ x-2y=11\end{array}\right.$

3. Déduire les solutions des systèmes suivants :

$$\begin{gathered} \overline{)1} \left(S_1\right):\left\{\begin{array}{l}-\sqrt{x}+\frac{3}{y}=4\\ \sqrt{x}-\frac{2}{y}=11\end{array}\right. \\ \overline{)2} \left(S_2\right):\left\{\begin{array}{l}-\left|x+1\right|+3y^2=4\\ \left|x+1\right|-2y^2=11\end{array}\right. \end{gathered}$$

V- Exercices

5-4/ Exercice 4

1. Résoudre dans $\mathrm{ℝ}$ l’équation suivante : $2x^2-2x-4=0$

2. Déduire les solutions de l'équation suivante : $2x^4-2x^2-4=0$

On considère l’équation suivante : $\left(E\right) : x^2+x-6=0$

3. Montrer que l’équation $\left(E\right)$ admet deux solutions distincts $\alpha$ et $\beta$ sans les calculer.

4. Calculer  $\alpha +\beta$, $\alpha \beta$, $\frac{1}{\alpha }+\frac{1}{\beta }$, $\alpha {\beta }^2+{\alpha }^2\beta$

5. Factoriser, si possible, les polynômes suivants :

$$\begin{gathered} P\left(x\right)=x^2-x-6 \\ Q\left(x\right)=\frac{1}{2}{x}^2+x+\frac{1}{2} \\ S\left(x\right)=x^2+3x+5 \end{gathered}$$