
الرياضيات أولى باك آداب وعلوم إنسانية
الحصة 2-1 (الحساب العددي والتناسبية – الدرس)
الأستاذ: شدادي هيثم
الفهرس
I- التناسبية
1-1/ النسبة المنوية
2-1/ التناسب والتناسب العكسي
II- المعادلات والمتراجحات والنظمات
1-2/ حل معادلة من الدرجة الأول بمجهول واحد
2-2/ حل معادلة من الدرجة الثانية بمجهول واحد
3-2/ حل نظمة معادلتين من الدرجة الأول بمجهولين6
I- التناسبية
1-1/ النسبة المنوية
تعريف
لتكن مجموعة عدد عناصرها ، و جزء من عدد عناصره .
النسبة المنوية التي تمثلها في هو العدد الذي بحقق : .
ونرمز له بالرمز .
مثال
عدد تلاميذ مؤسسة تعليمية هو تلميذ وعدد الإناث هو .
هي مجموعة التلاميذ في المؤسسة، والجزء هو مجموعة الفتيات.
النسبة المئوية التي تمثلها الفتيات هي :
يعني :
I- التناسبية
2-1/ التناسب والتناسب العكسي
تعريف 1 (التناسب)
و و و أعداد غير منعدمة.
يكون و متناسبين مع و إذا كان : .
مثال
I- التناسبية
2-1/ التناسب والتناسب العكسي
تعريف 2 (التناسب العكسي)
و و و أعداد غير منعدمة.
يكون و متناسبين عكسيا مع و إذا كان : ، يعني : .
مثال
II- المعادلات والمتراجحات والنظمات
1-2/ حل معادلة من الدرجة الأول بمجهول واحد
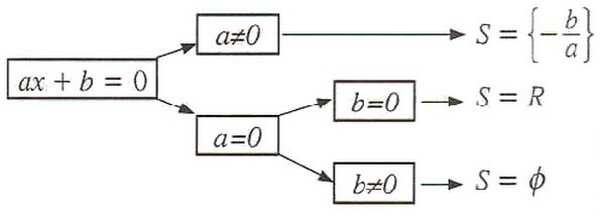
مثال
II- المعادلات والمتراجحات والنظمات
1-2/ حل معادلة من الدرجة الأول بمجهول واحد
إشارة

II- المعادلات والمتراجحات والنظمات
2-2/ حل معادلة من الدرجة الثانية بمجهول واحد
تسمى معادلة من الدرجة الثانية بمجهول واحد.
والعدد يسمى مميزها.
- إذا كان ، إذن المعادلة تقبل حلين مختلفين هما : و .
- إذا كان ، إذن المعادلة تقبل حلا وحيدا هو .
- إذا كان ، إذن المعادلة لا تقبل أي حل في .
مثال
II- المعادلات والمتراجحات والنظمات
2-2/ حل معادلة من الدرجة الثانية بمجهول واحد
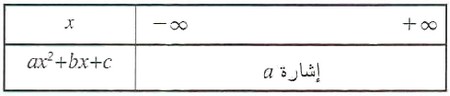
إشارة
- إذا كان :
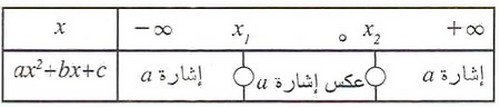
- إذا كان :

- إذا كان :
II- المعادلات والمتراجحات والنظمات
3-2/ حل نظمة معادلتين من الدرجة الأول بمجهولين
لحل النظمة يمكن استعمال الخوارزمية التالية :
1- نحسب المحددة :
2-
- إذا كان :
النظمة تقبل حلا وحيدا ، حيث و .
علما أن و .
- إذا كان :
أ- إذا كان أو ، فإن : .
ب- إذا كان ، فإن للنظمة ما لا نهاية له من الحلول، وتكون هذه الحلول مُحددة بإحدى المعادلتين.
مثال


