Séance 19C - Mouvements plans : Particule chargée dans un champ électrique

Sommaire

I- Mouvement d'une particule chargée dans un champs électrique uniforme

1-1/ Le champ électrique uniforme

1-2/ Déviation d'une particule chargée dans un champ électrique uniforme

1-3/ Étude du mouvement d'une particule chargée dans un champ électrique uniforme

II- Exercices

2-1/ Exercice 1

2-2/ Exercice 2

2-3/ Exercice 3

I- Mouvement d'une particule chargée dans un champs électrique uniforme

1-1/ Le champ électrique uniforme

Un champ électrique est dit uniforme s'il est constant en direction, en sens et en valeur : les lignes de champs sont alors toutes parallèles.

Les lignes de champ entre les plaques sont parallèles entre elles et perpendiculaires aux plans des plaques.

Le vecteur champ électrique $\overrightarrow{E}$ est orienté dans sens des potentielles décroissants (il est dirigé de la plaque ayant le plus grand potentiel vers celle ayant le plus petit potentiel).

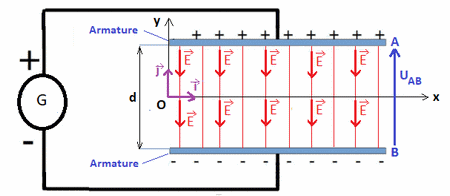
I- Mouvement d'une particule chargée dans un champs électrique uniforme

1-2/ Déviation d'une particule chargée dans un champ électrique uniforme

On utilise un tube de crookes qui contient un canon d'électrons qui permet d'obtenir un faisceau d'électrons ayant la même vitesse et à l'intérieur duquel il y'a un champ électrique uniforme.

Les électrons entrent dans le champ électrique avec une vitesse $\overrightarrow{v_0}$ perpendiculaire à $\overrightarrow{E}$.

On constate expérimentalement que la trajectoire du faisceau d'électrons est parabolique.

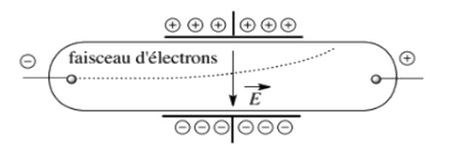
I- Mouvement d'une particule chargée dans un champs électrique uniforme

1-3/ Étude du mouvement d'une particule chargée dans un champ électrique uniforme

Les équations horaires du mouvement

En négligeant le poids, l'électron n'est soumis dans le champ électrique qu'à l'action de la force électrique : $\overrightarrow{F}=q\overrightarrow{E}=-e\overrightarrow{E}$

$\overrightarrow{F}$ et $\overrightarrow{E}$ ont des sens contraires.

$$\begin{gathered} \sum _{}^{}F=m\overrightarrow{a_G}=-e.\overrightarrow{E} \\ \Rightarrow \left\{\begin{array}{l}{a}_x=0\\ a_y=\frac{e.E}{m}\end{array}\right. \\ \Rightarrow \left\{\begin{array}{l}{v}_x=v_0\\ v_y=\frac{e.E}{m}t\end{array}\right. \\ \Rightarrow \left\{\begin{array}{l}x=v_{0}t\\ y=\frac{1}{2}\frac{e.E}{m}{t}^2\end{array}\right. \end{gathered}$$

I- Mouvement d'une particule chargée dans un champs électrique uniforme

1-3/ Étude du mouvement d'une particule chargée dans un champ électrique uniforme

L’équations de la trajectoire

$$\begin{gathered} \left\{\begin{array}{l}x=v_{0}t\\ y=\frac{1}{2}\frac{e.E}{m}{t}^2\end{array}\right. \\ \Rightarrow t=\frac{x}{v_0} \\ \Rightarrow \overline{) y=\frac{1}{2}\frac{e.E}{m.{v_0}^2}{x}^2 } \end{gathered}$$

I- Mouvement d'une particule chargée dans un champs électrique uniforme

1-3/ Étude du mouvement d'une particule chargée dans un champ électrique uniforme

Coordonnées du point de sortie de l'électron du champ électrique

$S$ est le point de sortie de l'électron $x_S=\mathcal{l}$.

En remplaçant dans $y$ on obtient : $y_S=\frac{e.E}{2m}\frac{{\mathcal{l}}^2}{{v_0}^2}$

Vitesse de l'électron lorsqu'il quitte le champ électrique

Le temps mis par l'électron pour arriver au point $S$ est $t=\frac{\mathcal{l}}{v_0}$

Donc $$\begin{gathered} V_S\left\{\begin{array}{l}{V}_{S_x}=v_0\\ V_{S_y}=\frac{e.E}{m}.\frac{\mathcal{l}}{v_0}\end{array}\right. \\ \Rightarrow tg\alpha =\frac{V_{S_y}}{V_{S_x}}=\frac{e.E.\mathcal{l}}{m.{v_0}^2} \end{gathered}$$

I- Mouvement d'une particule chargée dans un champs électrique uniforme

1-3/ Étude du mouvement d'une particule chargée dans un champ électrique uniforme

Déflexion électrique

Après sa sortie du champ électrique l'électron a un mouvement rectiligne uniforme jusqu'à ce qu'il rencontre l'écran au point P :

$$\begin{gathered} \left\{\begin{array}{l}tg\alpha =\frac{e.E}{m}.\frac{\mathcal{l}}{{v_0}^2}\\ y_S=\frac{1}{2}\frac{e.E}{m}\frac{{\mathcal{l}}^2}{{v_0}^2}\end{array}\right. \\ \Rightarrow x=\frac{y_S}{tg\alpha }=\frac{\mathcal{l}}{2} \end{gathered}$$

On appelle déflexion électrique la distance $D_e$ entre le point d’impact $O\text{'}$ de la particule avec l’écran en absence du champ électrique et le point d’impact $P$ de la particule avec l’écran en présence du champ électrique.

$$\begin{gathered} tg\alpha =\frac{y_S}{x}=\frac{D_e}{D} \\ \Rightarrow D_e=\frac{y_S.D}{x}=\frac{e.E}{m}\frac{\mathcal{l}.D}{{v_0}^2} \end{gathered}$$

Et on a $E=\frac{U}{d}$

Donc : $D_e=\frac{e.\mathcal{l}.D}{m.d.{v_0}^2}\times U=K\times U$

La déflexion électrique est proportionnelle à la tension entre les plaques.

II- Exercices

2-1/ Exercice 1

On applique entre deux plaques $\left(P_1\right)$ et $\left(P_2\right)$ une tension continue $U_0={10}^{4}V$.

On fait introduire au point $A$ un électron avec une vitesse $v_A\simeq 0$ et on espère l’accélérer pour qu’il puisse arriver au point B avec une vitesse $v_B$ :

1. Laquelle des deux plaques doit-on relier au pole positif du générateur pour qu’on puisse réaliser cette opération ? Justifier votre réponse.

2. En utilisant le théorème de l’énergie mécanique, trouver l’expression de la vitesse $v_B$. Calculer sa valeur.

Donnés : $e=1,6.{10}^{-19}C ; m_e=9,1.{10}^{-31}Kg$

II- Exercices

2-2/ Exercice 2

On considére deux plaques $\left(P_1\right)$ et $\left(P_2\right)$ parallèles entre eux et séparés d’une distance $d=4.0cm$ et ont chacune une longueur $\mathcal{l}=10cm$.

Un faisceau homocinétique (même vitesse) d’électrons rentrent entre les plaques par le point $O$, avec la vitesse $V_0=2,5.{10}^{3}Km/s$ et $\overrightarrow{V_0}=V_0.\overrightarrow{i}$:

Donnés : $e=1,6.{10}^{-19}C ; m_e=9,1.{10}^{-31}Kg$

1. Quelle est le signe de la tension $U$ qu’il faut appliquer entre $\left(P_1\right)$ et $\left(P_2\right)$ pour que le faisceau soit dévié vers le haut.

2. En appliquant entre $\left(P_1\right)$ et $\left(P_2\right)$ une tension $U=400V$, trouver l’équation de la trajectoire d’un électron dans le repère orthonormé $R(O,\overrightarrow{i},\overrightarrow{ j},\overrightarrow{k})$.

II- Exercices

2-3/ Exercice 3

Sélecteur de la vitesse (Principe)

Un sélecteur de vitesse est un appareil qui exploite simultanément le champ électrique $\overrightarrow{E}$ et le champ magnétique $\overrightarrow{B}$ pour séparer les ions selon leurs vitesses.

Dans cet appareil le champ $\overrightarrow{E}$ est perpendiculaire au champ $\overrightarrow{B}$, de telle façon que la somme vectorielle de la force électrique $\overrightarrow{F_e}$ et la force magnétique Fm est égale au vecteur nul pour l’ion de vitesse désigné $\left(\overrightarrow{F_e}+\overrightarrow{F_m}=\overrightarrow{0}\right)$, c’est pourquoi cet ion suit un mouvement rectiligne uniforme selon le principe d’inertie pour sortir d’un trou $O$ percé dans l’appareil.

Les autres ions pour lesquels $\left(\overrightarrow{F_e}+\overrightarrow{F_m}\ne \overrightarrow{0}\right)$ vont avoir des trajectoires quelconque pour rester à l’intérieur de l’appareil.

Application

On dispose d’un appareil permettant de produire des ions du néon 22  ${}_{10}{}^{22}N{e}^{+}$ et du néon 20 ${}_{10}{}^{20}N{e}^{+}$ à partir des atomes du néon. Après la sortie de ces ions de la chambre d’ionisation du point $O_1$ avec une vitesse pratiquement nulle, ils sont accélérés par une tension $U$, ce qui leurs permet de s’introduire dans une chambre où règne un champ magnétique $\overrightarrow{B}$ uniforme et perpendiculaire à un autre champs électrique uniforme $\overrightarrow{E}$, avec une vitesse $\overrightarrow{v}$ perpendiculaire à $\overrightarrow{E}$ et $\overrightarrow{B}$ au même temps.

On admet que le poids des ions $N{e}^{+}$ est négligeable devant la force électrostatique $\overrightarrow{F_e}$ et la force magnétique $\overrightarrow{F_m}$.

1. Donner l’expression de la force $\overrightarrow{F_e}$ et $\overrightarrow{F_m}$ appliquées à chaque ion après leurs introduction dans la zone où règne $\overrightarrow{E}$ et $\overrightarrow{B}$. Représenter $\overrightarrow{F_e}$ et $\overrightarrow{F_m}$ sur un schéma.

2. Calculer la vitesse des ions ${}_{10}{}^{22}N{e}^{+}$ et ${}_{10}{}^{20}N{e}^{+}$ lorsqu’ils arrivent au trou $O_2$.

3. Trouver la valeur de l’intensité du champ électrique $\overrightarrow{E}$, pour que les ions ${}_{10}{}^{22}N{e}^{+}$ puissent sortir seuls par le trou $O$ appartenant à l’axe $x’x$.

4. Quel est l’intérêt de cet appareil ?

Donnés

$$\begin{gathered} e=1,6.{10}^{-19C} ; M\left({}_{10}{}^{20}N{e}^{+}\right)=20g/mol \\ M\left({}_{10}{}^{22}N{e}^{+}\right)=22g/mol ; u=2.{10}^{4}V \\ {N}_A=6,02.{10}^{23}mo{l}^{-1} ; B=0,12T \end{gathered}$$